Question

Four identical electrical lamps are labelled $1.5 V$, $0.5 A$ which describes the condition necessary for them to operate at normal brightness. A $12 V$ battery of negligible internal resistance is connected to lamps as shown, then

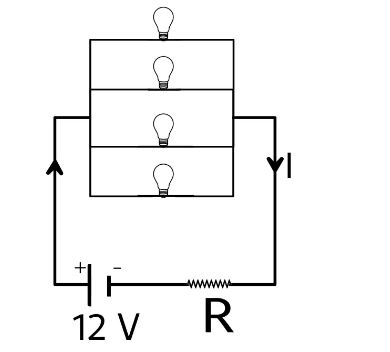
A. The value of $R$ for normal brightness of each lamp is $\dfrac{3}{4}\Omega$
B. The value of $R$ for normal brightness of each lamp is $\dfrac{{21}}{4}\Omega$
C. Total power dissipated in the circuit when all lamps are normally bright is $24W$.
D. Power dissipated in $R$ is $21W$ when all lamps are normally bright.

Answer 1

Here the current value and the voltage value for the normal brightness of the bulb is given, so we can add up the current value of the current passing through each bulb to get the total current through the battery, as these bulbs are parallel to each so their current values get added. Since we have the current value and the voltage value is given, we can conclude that power is dissipated by each bulb.

Formulas used:
$P = VI$
Where $P$ is the power, $V$ is the voltage and $I$ is the current value.
$V = IR$
Where $V$ is the voltage, $I$ is the current and $R$ is the resistance value.

Complete step by step answer:

Here we have replaced each of the bulbs with a resistance value of $K$. Now we need $0.5A$ of the current through each of the bulb for normal brightness
So total current through the circuit for normal brightness is $= 0.5 \times 4 = 2A$
The total voltage required for normal brightness $= 1.5V$
Since the connections are in parallel, the voltage will be equal for all the bulbs.
Voltage value through the resistance $R$ is $= 12 - 1.5 = 10.5V$

Now we have the voltage $10.5V$ left and the current through the resistance is $2A$. So, the maximum value of resistance is,
$R = \dfrac{V}{I} \\\ \Rightarrow R = \dfrac{{10.5}}{2} \\\ \Rightarrow R = \dfrac{{21}}{4}\Omega$
Now, power dissipated through resistance $R$ is $= VI = 10.5 \times 2 = 21\,W$
And power dissipated through all the bulb $= 4 \times \left( {1.5 \times 0.5} \right) = 3\,W$
So, the total value of power dissipated$= 21 + 3 = 24\,W$

Therefore, the correct options are (B), (C) and (D).

Note: Now there is another way to determine the power is to find the resistance of each of the bulb and then we use the formula $\left( {P = {I^2}R} \right)$ where $I$ is the current and $R$ is the value of the resistance of each of the bulb. This process will give us the answer but this will be lengthy, and will take comparatively extra time.