Question

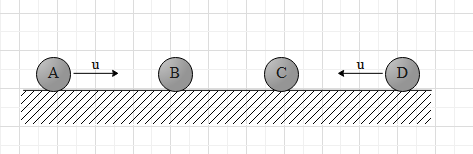
Four identical balls A, B, C and D are placed in line on a frictional horizontal surface. A and D are moved with the same speed ‘u’ towards the middle as shown. Assuming elastic collisions, find the final velocities.

Answer 1

Hint: Check whether the net force on the system during the collision is zero and use the law of conservation momentum. Also, it is given that the collisions are elastic, which means that law of conservation of kinetic energy is also applicable. Divide the question into different cases and analyse one by one.

Formula used:
p=mv
$K=\dfrac{1}{2}m{{v}^{2}}$

Complete step by step answer:
If we see the given figure, ball A will collide with ball B and ball D will collide with ball C.
Consider the collision between balls A and B. Since, there is no other except the forces of reaction, the net force on the system of these two balls is zero. Hence, we can you the law of conservation of momentum. Therefore, the initial momentum ${{P}_{i}}$ (before collision) of the system and the final momentum ${{P}_{f}}$ (after collision) of the system are equal.
Before the collision, the velocity of the ball A is u towards right and the ball B is at rest. The masses of both the balls are the same and let it be m.

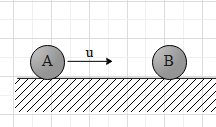
Therefore, ${{P}_{i}}=mu$
After the collision, let the ball A move with velocity ${{v}_{A}}$ and let the ball B move with velocity ${{v}_{B}}$.

Therefore, ${{P}_{f}}=m{{v}_{A}}+m{{v}_{B}}$
And ${{P}_{i}}={{P}_{f}}$
$\Rightarrow mu=m{{v}_{A}}+m{{v}_{B}}$
$\Rightarrow u={{v}_{A}}+{{v}_{B}}$ … (i).
It is given that the collision is elastic. Hence, the kinetic energy of the system is conserved.
That is the initial kinetic energy (before collision) and the final kinetic energy (after collision) of the system is the same.
The initial kinetic energy is ${{K}_{i}}=\dfrac{1}{2}m{{u}^{2}}$
And the final kinetic energy will be ${{K}_{f}}=\dfrac{1}{2}mv_{A}^{2}+\dfrac{1}{2}mv_{B}^{2}$.
And ${{K}_{i}}={{K}_{f}}$
$\Rightarrow \dfrac{1}{2}m{{u}^{2}}=\dfrac{1}{2}mv_{A}^{2}+\dfrac{1}{2}mv_{B}^{2}$
$\Rightarrow {{u}^{2}}=v_{A}^{2}+v_{B}^{2}$ …. (ii).
From equation (i) we get,
${{v}_{A}}=u-{{v}_{B}}$ ….. (iii).
Substitute this value in equation (ii).
$\Rightarrow {{u}^{2}}={{\left( u-{{v}_{B}} \right)}^{2}}+v_{B}^{2}$
$\Rightarrow {{u}^{2}}={{u}^{2}}-2u{{v}_{B}}+v_{B}^{2}+v_{B}^{2}$
$\Rightarrow 0=-u{{v}_{B}}+v_{B}^{2}$
$\Rightarrow 0={{v}_{B}}(-u+{{v}_{B}})$
This implies that ${{v}_{B}}=0$ or ${{v}_{B}}-u=0$
If ${{v}_{B}}=0$, then from equation (iii) ${{v}_{A}}=u$.
But how can the ball in front be at rest and the behind ball is moving in the same direction. Hence, ${{v}_{B}}=0$ is discarded
Therefore, ${{v}_{B}}-u=0\Rightarrow {{v}_{B}}=u$
This implies that ${{v}_{A}}=0$.
This means that after the collision, ball A comes to rest and the ball B will move with speed u in the right direction.

Before collision:

After collision:

We use a similar method and can correspond this to the collision between the balls C and D.
Here, before collision, the velocity of ball D is –u and after the collision ball D will be at rest and ball C will move with velocity –u.

Before collision:

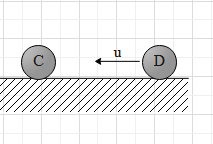
After collision:

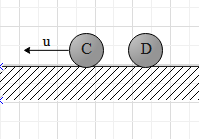
Now, the balls B and C will collide. Here also the net force on the system is zero. Therefore, use the law of conservation of momentum.

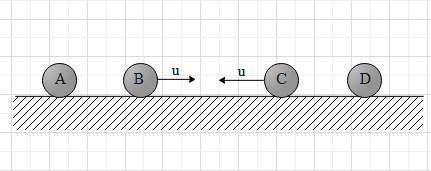
Here, ${{P}_{i}}=mu-mu=0$
After collision, let the velocity of the ball B be $v{{'}_{B}}$ and velocity of ball C be $v{{'}_{C}}$.

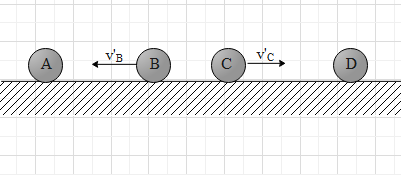
Therefore, ${{P}_{f}}=mv{{'}_{B}}+mv{{'}_{C}}$
And ${{P}_{i}}={{P}_{f}}$
$\Rightarrow 0=mv{{'}_{B}}+mv{{'}_{C}}$
$\Rightarrow 0=v{{'}_{B}}+v{{'}_{C}}$
$\Rightarrow v{{'}_{B}}=-v{{'}_{C}}$ ….. (iv).
The collision is elastic. Hence, law of conservation of kinetic energy is applicable.
Here, ${{K}_{i}}=\dfrac{1}{2}m{{u}^{2}}+\dfrac{1}{2}m{{u}^{2}}=m{{u}^{2}}$
${{K}_{f}}=\dfrac{1}{2} m{v_{B}^{2}}’+\dfrac{1}{2} m{v_{C}^{2}}’$
And ${{K}_{i}}={{K}_{f}}$
$\Rightarrow m{{u}^{2}}=\dfrac{1}{2}m{v_{B}^{2}}’+\dfrac{1}{2}m{v_{C}^{2}}’$
And $v{{'}_{B}}=-v{{'}_{C}}$
Therefore,
$\Rightarrow m{{u}^{2}}=\dfrac{1}{2}m{{{({(-v)}_{C})}^{2}}}’+\dfrac{1}{2}m{v_{C}^{2}}’$
$\Rightarrow m{{u}^{2}}=\dfrac{1}{2}m{v_{C}^{2}}’+\dfrac{1}{2}m{v_{C}^{2}}’=m{v_{C}^{2}}’$
$\Rightarrow {{u}^{2}}={v_{C}^{2}}’$
$\Rightarrow v{{'}_{C}}=\pm u$
If $v{{'}_{C}}=-u$ then from equation (iv), $v{{'}_{B}}=+u$. However, this is not possible. Hence, $v{{'}_{C}}=-u$ is discarded.
Hence, $v{{'}_{C}}=+u$ and $v{{'}_{B}}=-u$.
This means that after collision, ball B moves with speed u in the left direction and ball C with speed u in the right direction.
Now ball B will collide with ball A with speed u. We already have dealt with this kind of scenario and we know that after collision, ball B will stay at rest and ball A will move towards left with speed u.
Similarly, ball C will collide with ball D and ball C will stay at rest and ball D will move towards right with speed u.
Hence, the final velocities of balls A, B, C and D are –u, 0, 0, +u respectively.

Note: When we come across a problem which involves collision, we can use a formula as a shortcut.
It is a coefficient of restitution (e). It is defined as the ratio of the final to initial relative between the two bodies. For two bodies A and B having one dimensional collision $e=\dfrac{{{v}_{b}}-{{v}_{a}}}{{{u}_{a}}-{{u}_{b}}}$.
Here, ${{u}_{a}}$ is the velocity of body A before collision.
${{u}_{b}}$ is the velocity of body B before collision.
${{v}_{a}}$ is the velocity of body A after collision.
${{v}_{b}}$ is the velocity of body B after collision.
The value of e ranges from 0 to 1. For an elastic collision e=1.
Let us try for the collision between ball A and ball B.
Therefore, $e=1=\dfrac{{{v}_{B}}-{{v}_{A}}}{u}$.
$\Rightarrow u={{v}_{B}}-{{v}_{A}}$
And from the law of conservation of momentum we found $u={{v}_{A}}+{{v}_{B}}$.
With these two equations, we get that ${{v}_{B}}=u$ and ${{v}_{A}}=0$.