Question
Question: Four holes of radius R are cut from a thin square plate of side 4R and mass M. The moment of inertia...
Four holes of radius R are cut from a thin square plate of side 4R and mass M. The moment of inertia of the remaining portion about z-axis is
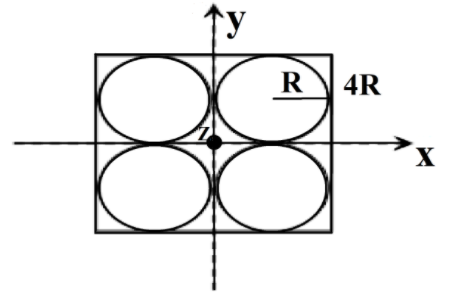
A. 12πMR2
B. (34−4π)MR
C. (34−4π)MR2
D. (38−1610π)MR2
Solution
While solving this question, go through each shape and part step by step. First find out the moment of inertia of the whole plate and then moment of inertia of one circle. Combined moment of inertia of four circles will be four times the MI of one circle.
Complete answer:
Let us take a look at all the given parameters,
Radius of each circular hole = R
length of side of the square sheet = L = 4R
Now,
Moment of inertia of the whole sheet about z-axis will be
Iz=6ML2
⇒Iz=6M(4R)2⇒Iz=38MR2
Now,
Mass of sheet = M
And, Area of one circle, A=πR2
Mass of each circle, m1=(4R)2M×πR2=16πM
Now,
Moment of inertia of the hole about centre,
