Question

Four equal point charges each of $16\,\mu C$ are placed on the four corners of a square of side ${\text{0}}{\text{.2}}\,{\text{m}}$. Calculate the force on any of the charges.

Answer 1

We are asked here to find the force on any of the charges on the corners of the square. Here, you will need to use coulomb’s law to find the force between two charges. Use this law to find the force exerted on any one point charge due to the other three charges. Then find the resultant force exerted on a point charge.

Complete step by step answer:
Given, charge on four corners of a square is, $Q = 16\,\mu C = 16 \times {10^{ - 6}}\,{\text{C}}$
Side of the square, $d = {\text{0}}{\text{.2}}\,{\text{m}}$
Here, we will use coulomb’s law, which states force between two charges is given as,
$F = \dfrac{{k{q_1}{q_2}}}{{{r^2}}}$ ……………(i)
where ${q_1}$ and ${q_2}$ are the two charges, $r$ is the distance between the centre of two charges and $k$ is the proportionality constant.

Let ABCD be the square with side $d = {\text{0}}{\text{.2}}\,{\text{m}}$ and point charge $Q = 16\,\mu C$ on each corner of the square.
We draw the diagram with the given information.

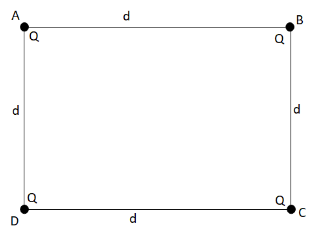
We are asked to calculate the force on any of the charges. The force on any of the charges will be the same.
Let us calculate the force on point A. We will now see the force exerted by the other three points on point A.Force exerted by point B on point A, using coulomb’s law from equation (i) we get,
${F_{BA}} = \dfrac{{kQQ}}{{{d^2}}} = \dfrac{{k{Q^2}}}{{{d^2}}}$ ………(ii)
force exerted by point D on point A, using coulomb’s law from equation (i) we get,
${F_{DA}} = \dfrac{{kQQ}}{{{d^2}}} = \dfrac{{k{Q^2}}}{{{d^2}}}$ …………(iii)
To find the force exerted by point C on point A, we need to find the distance between point A and C that is the length of the diagonal of the square.
We have the formula for length of diagonal of a square as,
$D = \sqrt 2 a$ where $a$ is the side of the square.
Here side of the square is $d$ so, the length of the diagonal will be
$D = \sqrt 2 d$

We redraw the diagram using this length of the diagonal.

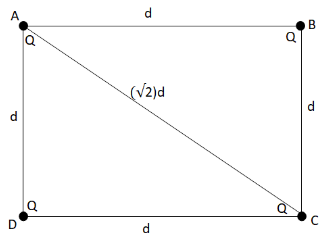
Now, force exerted by point C on point A using coulomb’s law from equation (i), we get
${F_{CA}} = \dfrac{{kQQ}}{{{{\left( {\sqrt 2 d} \right)}^2}}}$
$\Rightarrow {F_{CA}} = \dfrac{{k{Q^2}}}{{2{d^2}}}$ (iv)
Now, we can find the total force exerted on point A by adding the force exerted by the other three points.
Now, we draw the diagram with the forces ${F_{BA}}$, ${F_{DA}}$ and ${F_{CA}}$ which are along BA, DA and CA respectively.

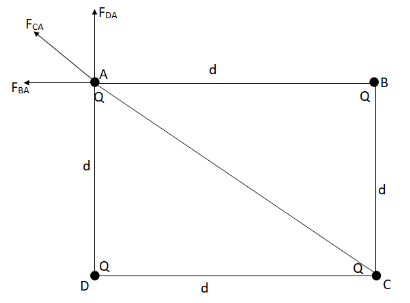
The resultant of forces ${F_{BA}}$ and ${F_{DA}}$ will be along CA, the resultant of forces ${F_{BA}}$ and ${F_{DA}}$ is
$F' = \sqrt {{F_{BA}}^2 + {F_{DA}}^2}$
Putting the values of ${F_{BA}}$ and ${F_{DA}}$ we get,
$F' = \sqrt {{{\left( {\dfrac{{k{Q^2}}}{{{d^2}}}} \right)}^2} + {{\left( {\dfrac{{k{Q^2}}}{{{d^2}}}} \right)}^2}}$
$\Rightarrow F' = \sqrt 2 \dfrac{{k{Q^2}}}{{{d^2}}}$ (v)
The forces $F'$ and ${F_{CA}}$ are along same direction, so the net force on point A will be addition of these two forces that is,
${F_{net}} = F' + {F_{CA}}$
Putting the values of $F'$ and ${F_{CA}}$, we get
${F_{net}} = \sqrt 2 \dfrac{{k{Q^2}}}{{{d^2}}} + \dfrac{{k{Q^2}}}{{2{d^2}}}$
$\Rightarrow {F_{net}} = \left( {\sqrt 2 + \dfrac{1}{2}} \right)\dfrac{{k{Q^2}}}{{{d^2}}}$
Now, putting the values of $Q$ , $d$ and $k = 9 \times {10^9}\,{\text{N}}{{\text{m}}^{\text{2}}}{{\text{C}}^{{\text{ - 2}}}}$ we get,
${F_{net}} = \left( {\sqrt 2 + \dfrac{1}{2}} \right)\dfrac{{\left( {9 \times {{10}^9}} \right){{\left( {16 \times {{10}^{ - 6}}} \right)}^2}}}{{{{\left( {0.2} \right)}^2}}}$
$\Rightarrow {F_{net}} = \left( {\dfrac{{2\sqrt 2 + 1}}{2}} \right)\dfrac{{9 \times 256 \times {{10}^{ - 3}}}}{{0.04}}$
$\Rightarrow {F_{net}} = \left( {2\sqrt 2 + 1} \right) \times 9 \times 32 \times {10^{ - 1}}$
$\ therefore{F_{net}} = 110.3\,{\text{N}}$

Therefore, the force on any charge will be $110.3\,{\text{N}}$.

Note: We have used the coulomb’s law. Coulomb states that force between two charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between the centers of the two charges. If the distance between the charges is increased the force between them reduces and if the distance between the charges is reduced the force between them increases.