Question

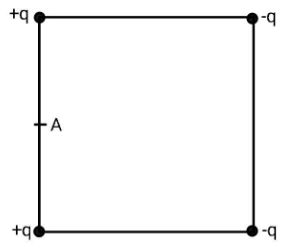
Four electric charges $+ q, + q, - q\,\& \,- q$ are placed at the corners of a square of side $2L$ (see figure). The electric potential at point A, midway between the two charges $+ q$ and $+ q$ is

(A) $\dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{2q}}{L}\left( {1 + \sqrt 5 } \right)$
(B) $\dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{2q}}{L}\left( {1 + \dfrac{1}{{\sqrt 5 }}} \right)$
(C) $\dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{2q}}{L}\left( {1 - \dfrac{1}{{\sqrt 5 }}} \right)$
(D) zero

Answer 1

Here, you are given four charges which are placed at the corners of a square of side $2L$ and you are supposed to find the potential at point A due to these four charges. For general purpose, calculate the electric potential due to a point charge at a distance $r$. After finding this, you find electric potential due to individual charge and then sum it up in order to find the net electric potential at the point A.

Complete step by step answer:
The electric potential at any point is defined as the electric potential energy per unit charge, mathematically, we have electric potential as $V = \dfrac{U}{q}$, where $q$ is the test charge.Consider a point charge having charge $q$ which is at origin. Now, consider another point charge ${q_0}$ which is at infinity. This charge ${q_0}$ is under the influence of the electric field of charge $q$.

Let us bring the charge ${q_0}$ from infinity to position vector ${\mathbf{r}}$. Obviously, work needs to be done against the electric field in order to change the configuration of the system or say position of the charge ${q_0}$.The force on the charge ${q_0}$ is $F = \dfrac{{kq{q_0}}}{{{r^2}}}$, where $k = \dfrac{1}{{4\pi {\varepsilon _0}}}$.
Work done will be given as
W = \int {dW} = \int\limits_\infty ^r {Fdr} \\\ \Rightarrow W = \int\limits_\infty ^r {\dfrac{{kq{q_0}}}{{{r^2}}}dr} \\\ \Rightarrow W = kq{q_0}\int\limits_\infty ^r {\dfrac{1}{{{r^2}}}dr} \\\ \Rightarrow W = kq{q_0}\left[ { - \dfrac{1}{r}} \right]_\infty ^r \\\ \Rightarrow W = - kq{q_0}\left( {\dfrac{1}{r} - \dfrac{1}{\infty }} \right) \\\ \Rightarrow W = - \dfrac{{kq{q_0}}}{r} \\\
The change in potential energy is given as
{U_f} - {U_i} = - W = - \left( { - \dfrac{{kq{q_0}}}{r}} \right) \\\ \Rightarrow {U_f} - {U_i} = \dfrac{{kq{q_0}}}{r} \\\
We take the potential energy at infinity to be zero, $\to {U_i} = 0$ and therefore, potential energy at the position vector ${\mathbf{r}}$ is given by $U = \dfrac{{kq{q_0}}}{r}$.
As discussed before, electric potential is defined as potential energy per unit charge. Hence, potential due to a point charge at any point is given as$V = \dfrac{{kq}}{r}$.
So, electric potential due to top left charge will be ${V_1} = \dfrac{{kq}}{{\dfrac{{2L}}{2}}} = \dfrac{{kq}}{L}$. Similarly, electric potential due to bottom left charge will be ${V_2} = \dfrac{{kq}}{L}$. Electric potential due to top right point charge will be ${V_3} = \dfrac{{k\left( { - q} \right)}}{{\sqrt {{{\left( {\dfrac{{2L}}{2}} \right)}^2} + {{\left( {2L} \right)}^2}} }} = - \dfrac{{kq}}{{\sqrt 5 L}}$. As the bottom right point charge is identical to the top right point charge, the potential due to that charge will also be equal to ${V_4} = - \dfrac{1}{{\sqrt 5 }}\dfrac{{kq}}{L}$.

The net electric potential of the system will be
V = \sum\limits_{i = 1}^4 {{V_i}} = {V_1} + {V_2} + {V_3} + {V_4} \\\ \Rightarrow V = \dfrac{{kq}}{L} + \dfrac{{kq}}{L} + \left( { - \dfrac{1}{{\sqrt 5 }}\dfrac{{kq}}{L}} \right) + \left( { - \dfrac{1}{{\sqrt 5 }}\dfrac{{kq}}{L}} \right) \\\ \Rightarrow V = \dfrac{{2kq}}{L}\left( {1 - \dfrac{1}{{\sqrt 5 }}} \right) \\\
As $k = \dfrac{1}{{4\pi {\varepsilon _0}}}$, we have, $V = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{2q}}{L}\left( {1 - \dfrac{1}{{\sqrt 5 }}} \right)$.
Therefore, the electric potential at point A, midway between the two charges $+ q$ and $+ q$ is $\dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{2q}}{L}\left( {1 - \dfrac{1}{{\sqrt 5 }}} \right)$.

Hence, option C is correct.

Note: Here, we have discussed in detail about the electric potential, electric potential energy, work done, force on a charged particle due to some other charged particle. The force due to charge on another charge is given by Coulomb's law. You need to memorize all the definitions and formulae of each term used in this solution.