Question

Four different capacitors are connected in series then

Answer 1

In a number of applications, several capacitors can be linked together. Multiple capacitor connections behave as though they were a single equivalent capacitor. The overall capacitance of this equivalent single capacitor is determined by the individual capacitors as well as the connections between them. The total capacitance of two basic and popular types of connections, called series and parallel, may be simply calculated. Combinations of series and parallel can also be used to explain more complex relationships.

Complete step by step answer:
A capacitor is an electrical energy storage device that operates in an electric field. It's a two-terminal passive electrical component. Capacitance is the term used to describe the effect of a capacitor. While there is some capacitance between any two electrical conductors in close proximity in a circuit, a capacitor is a component that is specifically intended to provide capacitance to a circuit. Originally, the capacitor was known as a condenser or condenser.
The schematic design, when connected in series, demonstrates that the separation distance, not the plate area, adds up. Each capacitor in the series stores the same amount of instantaneous charge build-up as the others in the series. The inverse of each capacitor's capacitance is used to distribute the overall voltage difference from end to end. The entire series functions as a capacitor with a lesser capacitance than any of its individual components.

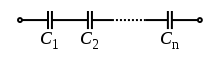
here we have 4 capacitor so
$\dfrac{1}{{{C_{{\text{eq}}}}}} = \sum\limits_i {\dfrac{1}{{{C_i}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \cdots + \dfrac{1}{{{C_n}}}$
$\dfrac{1}{{{C_{{\text{eq}}}}}} = \sum\limits_4 {\dfrac{1}{{{C_4}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \cdots + \dfrac{1}{{{C_4}}}$

Note:
Capacitors are connected in series to generate a greater operating voltage, which is useful for smoothing a high-voltage power supply, for example. If the capacitance and leakage currents for each capacitor are the same, the voltage ratings, which are dependent on plate separation, total up. In this case, series strings are sometimes linked in parallel to form a matrix. The objective is to optimise the network's energy storage while avoiding overloading any capacitors. When using capacitors in series for high-energy storage, various safety precautions must be taken to guarantee that if one capacitor fails, the leaking current does not apply too much voltage to the remaining series capacitors.