Question

Four containers are filled with monoatomic ideal gases. For each container, the number of moles, the mass of an individual atom and the rms speed of the atoms are expressed in terms of n, m and $V_{rms}$ respectively. If $T_A$, $T_B$, $T_C$ and $T_D$ are their temperatures respectively then which one of the options correctly represents the order ?

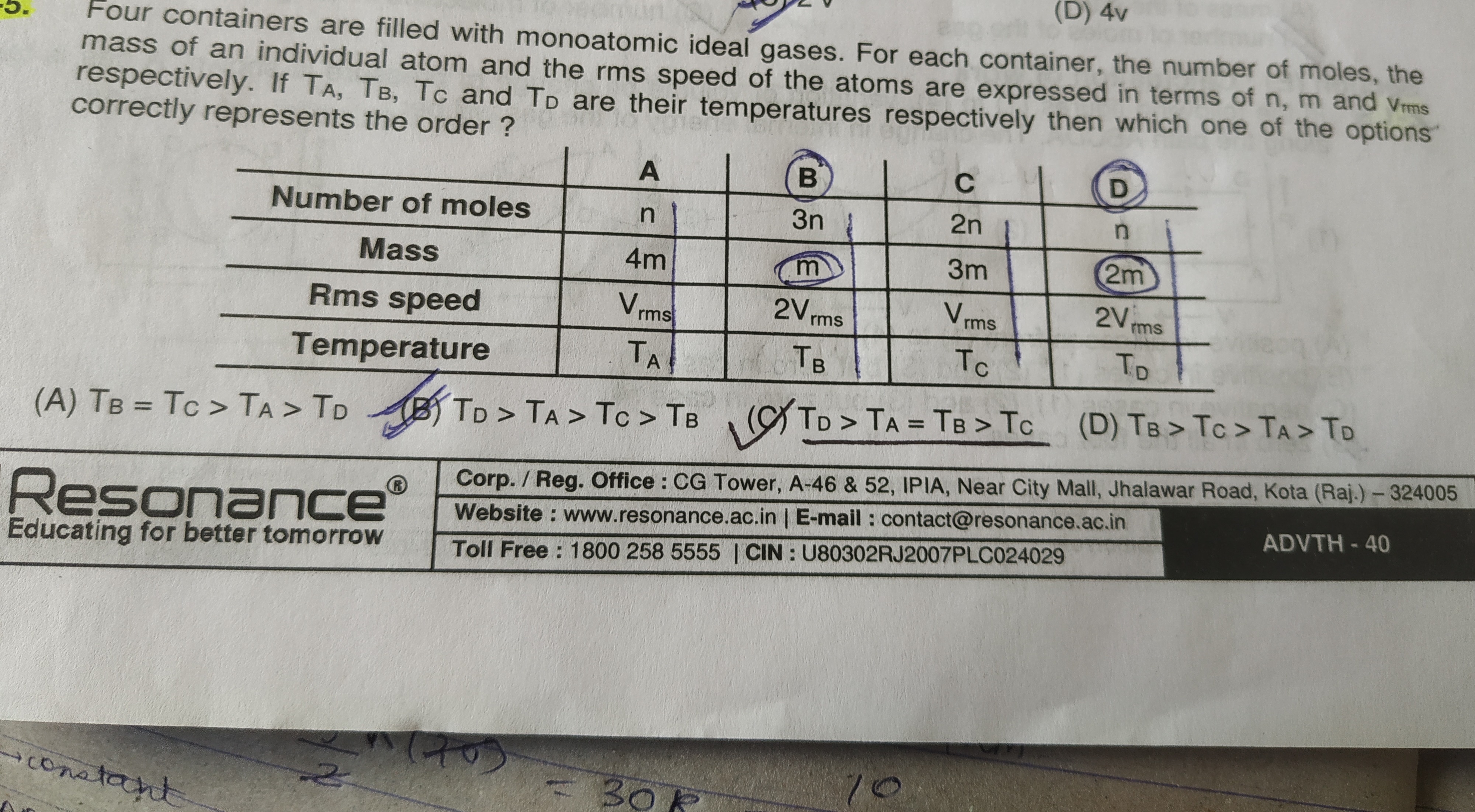
• A. $T_B=T_C>T_A>T_D$
• B. $T_D>T_A>T_C>T_B$
• C. $T_D>T_A=T_B>T_C$
• D. $T_B>T_C>T_A>T_D$

Answer 1

Answer: (C)

C

Answer 2

The root mean square (rms) speed of gas molecules is related to the absolute temperature (T) and the mass of an individual atom (m) by the formula:

$V_{rms} = \sqrt{\frac{3kT}{m}}$

where k is the Boltzmann constant.

Squaring both sides, we get:

$V_{rms}^2 = \frac{3kT}{m}$

Rearranging the formula to express temperature (T):

$T = \frac{m V_{rms}^2}{3k}$

Since 3k is a constant, the temperature T is directly proportional to the product of the mass of an individual atom (m) and the square of its rms speed ($V_{rms}^2$). So, we can write $T \propto m V_{rms}^2$.

Let's calculate the value of the product $m V_{rms}^2$ for each container (A, B, C, D) using the given data:

Container A: Mass of individual atom = $4m$ Rms speed = $V_{rms}$ Temperature factor $T_A' = (4m) \times (V_{rms})^2 = 4mV_{rms}^2$

Container B: Mass of individual atom = $m$ Rms speed = $2V_{rms}$ Temperature factor $T_B' = (m) \times (2V_{rms})^2 = m \times (4V_{rms}^2) = 4mV_{rms}^2$

Container C: Mass of individual atom = $3m$ Rms speed = $V_{rms}$ Temperature factor $T_C' = (3m) \times (V_{rms})^2 = 3mV_{rms}^2$

Container D: Mass of individual atom = $2m$ Rms speed = $2V_{rms}$ Temperature factor $T_D' = (2m) \times (2V_{rms})^2 = 2m \times (4V_{rms}^2) = 8mV_{rms}^2$

Now, let's compare these temperature factors: $T_A' = 4mV_{rms}^2$ $T_B' = 4mV_{rms}^2$ $T_C' = 3mV_{rms}^2$ $T_D' = 8mV_{rms}^2$

From the comparison, we can see the order of temperatures: $T_D > T_A = T_B > T_C$

This order matches option (C). The number of moles information is not required for this calculation.