Question

Four condensers each of capacity $4\,\mu F$ are connected as shown in figure ${V_p} - {V_q} = 15\,V$. The energy stored in the system is:

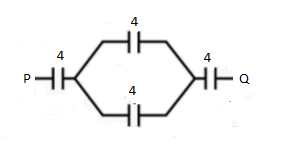
(A) $2400\,ergs$
(B) $1800\,ergs$
(C) $3600\,ergs$
(D) $5400\,ergs$

Answer 1

Hint In this question, from the given diagram two capacitance are in parallel, by using the capacitance in parallel formula for this two capacitors, then this two capacitors will become one capacitor, and the remaining two capacitors are in series with the combined capacitor of the two capacitance, so three capacitors are in series, by using the capacitance in series formula total capacitance is determined, then energy can be determined by energy of the capacitor formula.
Useful formula
The capacitance in series is given by,
$\dfrac{1}{C} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + ..............$
Where, $C$ is the total capacitance and ${C_1}$ and ${C_2}$ are the capacitance of the individual capacitors.
The capacitance in parallel is given by,
$C = {C_1} + {C_2} + .............$
Where, $C$ is the total capacitance and ${C_1}$ and ${C_2}$ are the capacitance of the individual capacitors.
The energy stored in the capacitor is given by,
$E = \dfrac{1}{2}C{V^2}$
Where, $E$ is the energy stored in the capacitor, $C$ is the capacitance of the capacitor and $V$ is the voltage in the capacitor.

Complete step by step solution
Given that,
All the capacitors are having same capacitance, ${C_1} = {C_2} = {C_3} = {C_4} = 4\,\mu F$
The voltage in the circuit is, $V = 15\,V$
Assume the name of the capacitors as the capacitor ${C_1}$ is series with the ${C_2}$, ${C_3}$ and ${C_4}$.
The capacitors ${C_2}$ and ${C_3}$ are in parallel.

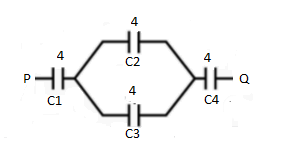
Now, by using the capacitor in parallel formula for ${C_2}$ and ${C_3}$, then
$C = {C_2} + {C_3}$
By substituting the capacitance of ${C_2}$ and ${C_3}$ in the above equation, then
$C = 4 + 4$
By adding the terms in the above equation, then the above equation is written as,
$C = 8\,\mu F$
Now the capacitors ${C_1}$, $C$ and ${C_4}$ are in series, then by using the capacitors in series formula, then
$\dfrac{1}{C} = \dfrac{1}{{{C_1}}} + \dfrac{1}{C} + \dfrac{1}{{{C_4}}}$
By substituting the capacitance of ${C_1}$, $C$ and ${C_4}$ in the above equation, then
$\dfrac{1}{C} = \dfrac{1}{4} + \dfrac{1}{8} + \dfrac{1}{4}$
By taking the LCM of the above equation, then
$\dfrac{1}{C} = \dfrac{{2 + 1 + 2}}{8}$
By adding the above equation, then
$\dfrac{1}{C} = \dfrac{5}{8}$
By taking reciprocal on the above equation, then
$C = \dfrac{8}{5}\,\mu F$
The energy stored in the capacitor is given by,
$E = \dfrac{1}{2}C{V^2}$
By substituting the total capacitance and the voltage in the above equation, then
$E = \dfrac{1}{2} \times \dfrac{8}{5} \times {15^2}$
By using the square in the above equation, then
$E = \dfrac{1}{2} \times \dfrac{8}{5} \times 225$
By multiplying the above equation, then
$E = \dfrac{{1800}}{{10}}$
By dividing the terms in the above equation, then
$E = 1800\,ergs$

Hence, the option (B) is the correct answer.

Note The energy stored in the capacitor is directly proportional to the total capacitance of the circuit and the voltage in the circuit. As the total capacitance or the voltage in the circuit increases, the energy stored by the capacitor also increases.