Question

Four concurrent coplanar forces in Newton are acting at a point and kept in equilibrium, then the values of $F$ and $\phi$ are:

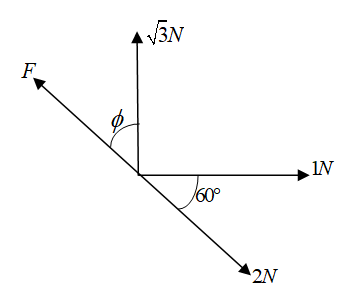
(A) $1N,60^\circ$
(B) $2N,60^\circ$
(C) $\sqrt 2 N,90^\circ$
(D) $2N,90^\circ$

Answer 1

Hint To solve this question, we need to resolve all the forces into the vertical and horizontal components. Then applying the condition of equilibrium in both the directions, we will get two equations. The magnitude of the force and the angle will be computed from these two equations.

Formula Used: The formula used in solving this question is given by
$\Rightarrow {\vec F_{net}} = {\vec F_1} + {\vec F_2} + ......$
Where, ${\vec F_{net}}$ is the net force after addition of the force vectors ${\vec F_1}$ , $\Rightarrow {\vec F_2}$.

Complete step by step answer
From the figure given in the question

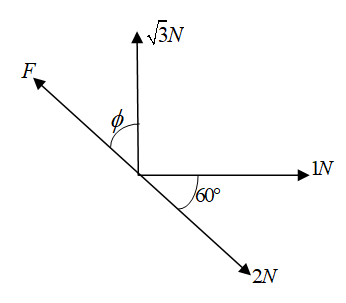
We first resolve all the forces in the horizontal and vertical components.

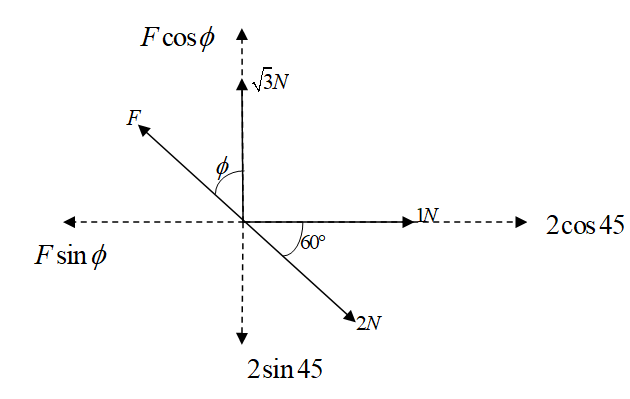
Now since the forces are in equilibrium, so the horizontal and vertical components of the forces must also be in equilibrium.
Now, since the horizontal components of the forces are in equilibrium, so the left hand side should be in equilibrium with the right hand side. Thus, we get,
$\Rightarrow F\sin \phi = 1 + 2\cos 60$
Similarly, since the vertical components of the forces are in equilibrium, so the upward and downward forces should be equal. So, we get,
$\Rightarrow F\cos \phi + \sqrt 3 = 2\sin 60$
Now, dividing the first equation by second equation we get,
$\Rightarrow \dfrac{{F\sin \phi }}{{F\cos \phi }} = \dfrac{{1 + 2\cos 60}}{{2\sin 60 - \sqrt 3 }}$
So, we get,
$\Rightarrow \tan \phi = \dfrac{{1 + 2\cos 60}}{{2\sin 60 - \sqrt 3 }} \\\ \Rightarrow \tan \phi = \dfrac{{1 + 2\left( {\dfrac{1}{2}} \right)}}{{2\left( {\dfrac{{\sqrt 3 }}{2}} \right) - \sqrt 3 }} \\\$
This gives us,
$\Rightarrow \tan \phi = \dfrac{{1 + 1}}{{\sqrt 3 - \sqrt 3 }} = \dfrac{2}{0} \\\ \Rightarrow \tan \phi \to \infty \\\$
This gives us,
$\phi = 90^\circ$
Now, putting this value in either of the first two equations above, we can get the value of the unknown force $F$ . So, let us put the value of $\phi$ in the first equation,
$\Rightarrow F\sin 90 = 1 + 2\cos 60 \\\ \Rightarrow F(1) = 1 + 2\left( {\dfrac{1}{2}} \right) \\\$
This finally gives us,
$F = 1 + 1 = 2N$
$\therefore$ Option (D) is the correct option out of the given options.

Note
We can also attempt this question by resolving all the forces and then calculating the net force in the horizontal direction. Then, checking each option for the pair which matches the value for the net force in the horizontal direction will give the final answer. This way, we can eliminate all the incorrect options quickly.