Question

Four charges +q each are placed at four corners of a square. A 5th charge Q is placed at the center of the square. Find Q such that the whole system is to be in equilibrium.

Answer 1

When the fifth charge is placed at the center then the system comes in equilibrium. Although all are charges, they must interact with each other through Coulombic attraction or repulsion, but the system is in equilibrium. So, in order to solve this problem, we find out all the forces acting on one particular charge and the resultant of all such forces will be equal to zero.

Complete step by step answer:

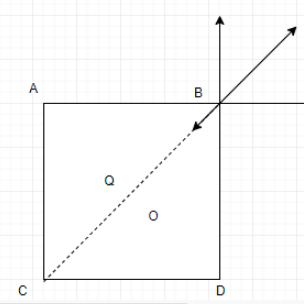
The square ABCD and at each corner the charge is +q. The charge Q is at the center of the square. All the charges at corner A, C, and D repel the charge at point B, represented by the arrows.Let us assume that the side of the square be a. Also, we know if the side of the square is a, then its diagonal will be $\sqrt{2}a$. Also, the diagonals of the square are equal and bisect each other at right angle, so OC= $\dfrac{a}{\sqrt{2}}$
Now, using Coulomb’s law to find out the electrostatic force:
${{F}_{AB}}=\dfrac{k{{Q}^{2}}}{{{a}^{2}}}\widehat{AB}$--(1)
${{F}_{DB}}=\dfrac{k{{Q}^{2}}}{{{a}^{2}}}\widehat{DB}$---(2)
${{F}_{CB}}=\dfrac{k{{Q}^{2}}}{{{(\sqrt{2}a)}^{2}}}\widehat{CB}$--(3)
Forces given by eq (1) and eq (2) are perpendicular to each other, so their resultant points in the direction of force given by eq (3),
${{F}_{res}}=\sqrt{{{(\dfrac{k{{Q}^{2}}}{{{a}^{2}}})}^{2}}+{{(\dfrac{k{{Q}^{2}}}{{{a}^{2}}})}^{2}}}$
\Rightarrow {{F}_{res}}=\dfrac{k{{Q}^{2}}}{{{a}^{2}}}\sqrt{2}$$$$\widehat{CB}---(4)
Now forces given by eq (4) and eq (3) are in same direction, so adding the two we get,
{{F}_{res}}=[\dfrac{k{{Q}^{2}}}{{{a}^{2}}}\sqrt{2}+\dfrac{k{{Q}^{2}}}{{{(\sqrt{2}a)}^{2}}}]\widehat{CB} \\\ \Rightarrow {{F}_{res}}=\dfrac{k{{Q}^{2}}}{{{a}^{2}}}[\sqrt{2}+\dfrac{1}{2}]\widehat{CB} \\\
Now this force must be equal to the force exerted by the charge at O for the system to remain in equilibrium. Thus the charge Q is of opposite polarity and thus,
$\dfrac{kQq}{{{(\dfrac{a}{\sqrt{2}})}^{2}}}=\dfrac{k{{Q}^{2}}}{{{a}^{2}}}[\sqrt{2}+\dfrac{1}{2}] \\\ \Rightarrow \dfrac{q}{{{(\dfrac{a}{\sqrt{2}})}^{2}}}=\dfrac{Q}{{{a}^{2}}}[\sqrt{2}+\dfrac{1}{2}] \\\ \Rightarrow \dfrac{2q}{{{a}^{2}}}=\dfrac{Q}{{{a}^{2}}}[\sqrt{2}+\dfrac{1}{2}] \\\ \Rightarrow 2q=Q[\sqrt{2}+\dfrac{1}{2}] \\\ \therefore q=\dfrac{Q}{4}(1+2\sqrt{2})$

Hence, putting the polarity sign, $q=-\dfrac{Q}{4}(1+2\sqrt{2})$.

Note: A stationary charge produces electric field around itself. The extent up to which the influence of the field can be felt depends up on the magnitude of the charge. When another charge is there, then the two charges attract or repel each other with a force which is directly proportional to the product of magnitude of two charges and inversely proportional to the square of distance between them.