Question

Four charges each equal to$Q$ are placed at the four corners of a square and a charge $q$ is placed at the centre of the square. If the system is in equilibrium, the value of $q$ is
(A) $\dfrac{Q}{2}\left( {1 + 2\sqrt 2 } \right)$
(B) $- \dfrac{Q}{4}\left( {1 + 2\sqrt 2 } \right)$
(C) $\dfrac{Q}{4}\left( {1 + 2\sqrt 2 } \right)$
(D) $- \dfrac{Q}{2}\left( {1 + 2\sqrt 2 } \right)$

Answer 1

Here, five charges are given out of which four charges of charge equal to $Q$ are placed at the corner of a square, let us say that the side is equal to $a$ and the fifth charge of charge $q$ is placed at the centre of the square and you are asked to find the value of charge . A condition is given to you, that is, the system is in equilibrium. So, if you take any charge present in the system, the force on the charge will be zero. Apply this condition and find the value of charge $q$.

Complete step by step answer:
First, let us find the force on a point charge due to another point charge. Consider two point charges, one having charge equal to ${q_1}$ and is placed at the origin and the other having charge equal to ${q_2}$ and is placed at a position vector ${\mathbf{r}}$. The force on charge ${q_2}$ due to charge ${q_1}$ is given by the Coulomb’s law, $F = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q_1}{q_2}}}{{{r^2}}}\widehat r$. It acts radially outward and along the line joining the two point charges. The system is as shown in the figure:

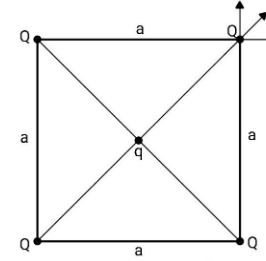
The direction of forces acting on the top right charge $Q$ is given. The net force on this charge has to be zero as the system is in equilibrium. The force will be given by ${F_Q} = {F_{Q \to Q}} + {F_{Q \to Q}} + {F_{Q \to Q}} + {F_{q \to Q}}$, where each force ${F_{Q \to Q}}$ is of different charges $Q$.

$${F_Q} = \left( {\dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{Q^2}}}{{{a^2}}}} \right)\widehat i + \left( {\dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{Q^2}}}{{{a^2}}}} \right)\widehat j + \left( {\dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{Q^2}}}{{\sqrt 2 {{\left( {\sqrt 2 a} \right)}^2}}}\widehat i + \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{Q^2}}}{{\sqrt 2 {{\left( {\sqrt 2 a} \right)}^2}}}\widehat j} \right) + \left( {\dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{qQ}}{{\sqrt 2 {{\left( {\dfrac{a}{{\sqrt 2 }}} \right)}^2}}}\widehat i + \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{qQ}}{{\sqrt 2 {{\left( {\dfrac{a}{{\sqrt 2 }}} \right)}^2}}}\widehat j} \right) \\\ \Rightarrow{F_Q} = \left( {\dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{Q^2}}}{{{a^2}}} + \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{Q^2}}}{{\sqrt 2 {{\left( {\sqrt 2 a} \right)}^2}}} + \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{qQ}}{{\sqrt 2 {{\left( {\dfrac{a}{{\sqrt 2 }}} \right)}^2}}}} \right)\widehat i + \left( {\dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{Q^2}}}{{{a^2}}} + \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{Q^2}}}{{\sqrt 2 {{\left( {\sqrt 2 a} \right)}^2}}} + \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{qQ}}{{\sqrt 2 {{\left( {\dfrac{a}{{\sqrt 2 }}} \right)}^2}}}} \right)\widehat j \\\$$

Now, this force is equal to zero and so will be each component of the force.

$$\dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{Q^2}}}{{{a^2}}} + \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{Q^2}}}{{\sqrt 2 {{\left( {\sqrt 2 a} \right)}^2}}} + \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{qQ}}{{\sqrt 2 {{\left( {\dfrac{a}{{\sqrt 2 }}} \right)}^2}}} = 0 \\\ \Rightarrow\dfrac{Q}{{4\pi {\varepsilon _0}{a^2}}}\left( {Q + \dfrac{Q}{{2\sqrt 2 }} + \dfrac{{2q}}{{\sqrt 2 }}} \right) = 0 \\\ \Rightarrow Q + \dfrac{Q}{{2\sqrt 2 }} + \dfrac{{2q}}{{\sqrt 2 }} = 0 \\\ \Rightarrow\dfrac{{2q}}{{\sqrt 2 }} = - Q\left( {\dfrac{{2\sqrt 2 + 1}}{{2\sqrt 2 }}} \right) \\\ \therefore q = - \dfrac{Q}{4}\left( {2\sqrt 2 + 1} \right) \\\$$

Therefore, if the system is in equilibrium, the value of $q$ is $- \dfrac{Q}{4}\left( {1 + 2\sqrt 2 } \right)$.

Hence, option B is correct.

Note: In the above question, we have discussed the force on a charged particle due to another charged particle. This force is actually due to the electric field produced by one charge and the other charge is in the influence of this produced field. The electric field is defined as force per unit charge. You should keep in mind the Coulomb’s law of electrostatics as it gives the magnitude and direction of the force between charges.