Question

Four charges are brought from infinity and placed at one meter intervals as shown. Determine the electric potential energy of this group?

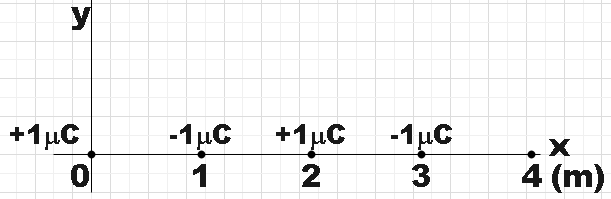
A. 0.068J
B. 0.032J
C. 0J
D. -0.014J
E. -0.021J

Answer 1

Firstly, you could recall the potential energy due to a system consisting of just two charges. Then, you could modify this expression for a system of 4 charges which would be the sum of the potential energies of all possible combinations. Substituting the values will give us the answer.
Formula used:
Potential energy of the system,
$U=k\left( \dfrac{{{q}_{1}}{{q}_{2}}}{1}+\dfrac{{{q}_{1}}{{q}_{3}}}{2}+\dfrac{{{q}_{1}}{{q}_{4}}}{3}+\dfrac{{{q}_{2}}{{q}_{3}}}{1}+\dfrac{{{q}_{2}}{{q}_{4}}}{2}+\dfrac{{{q}_{3}}{{q}_{4}}}{1} \right)$

Complete answer:
In the question, we are given a system of four charges that are kept at 1m distance between them and we are asked to find the electric potential energy of the group.
In order to find the net electric potential energy, let us recall the expression for the same when the system contains just two charges kept at r distance from each other. So, the expression will be,
$U=k\dfrac{{{q}_{1}}{{q}_{2}}}{r}$
Where, k is constant given by,
$k=9\times {{10}^{9}}N{{m}^{2}}{{C}^{-2}}$
Now, for a system of charges, the net potential energy will be given by the sum of the potential energies of all possible combinations. So, for the given system it will be,
$U=k\left( \dfrac{{{q}_{1}}{{q}_{2}}}{1}+\dfrac{{{q}_{1}}{{q}_{3}}}{2}+\dfrac{{{q}_{1}}{{q}_{4}}}{3}+\dfrac{{{q}_{2}}{{q}_{3}}}{1}+\dfrac{{{q}_{2}}{{q}_{4}}}{2}+\dfrac{{{q}_{3}}{{q}_{4}}}{1} \right)$
Substituting the values we get,
$\Rightarrow U=9\times {{10}^{9}}\left( \dfrac{1}{1}+\dfrac{1}{2}+\dfrac{-1}{3}+\dfrac{-1}{1}+\dfrac{1}{2}+\dfrac{-1}{1} \right)\times {{10}^{-12}}$
$\Rightarrow U=-\dfrac{9\times 7}{3}\times {{10}^{-3}}$
$\therefore U=-0.021J$
So, we have found the potential energy of the given system consisting of four charges arranged as shown to be -0.021J.

Hence, Option E is found to be the correct answer.

Note:
While substituting the distances one should be careful about noting down the exact distance between the charges in particular combination. The given system is such that it shows a possibility of mistaking the distance of separation to be 1m. Also, note that the signs of the charges do have significance in the expression.