Question

Four charges are arranged at the corners of a square as shown in the figure. The direction of electric field at the centre of the square is along:

Answer 1

Hint : The force of attraction or repulsion between two stationary point charges is directly proportional to the product of magnitude of charges and inversely proportionally to the square of the distance between them. And this net force acts along the line joining these two charges.
Formula Used:

Coulomb’s law of electrostatic force: $F = k\dfrac{{{q_1}{q_2}}}{{{r^2}}}$

where k is the electrostatic force constant,
${q_1}{\text{ and }}{q_2}$ represents the two static charges,
and r is the distance of separation between the two charges.

Complete step by step answer:
Coulomb’s Law of electric force stated that the force of attraction or repulsion between two stationary point charges is inversely proportionally to the square of the distance between them and directly proportional to the product of magnitude of charges. This resultant force acts along the line joining these two charges.
Mathematically,

\eqalign{ & F \propto {q_1}{q_2}{\text{ and }}F \propto \dfrac{1}{{{r^2}}} \cr & \Rightarrow F \propto \dfrac{{{q_1}{q_2}}}{{{r^2}}} \cr & \therefore F = k\dfrac{{{q_1}{q_2}}}{{{r^2}}} \cr}

where k is the electrostatic force constant,
${q_1}{\text{ and }}{q_2}$ represents the two static charges,
and r is the distance of separation between the two charges.
Let the given diagram be along a two dimensional coordinate system with x-axis along its horizontal and y along its vertical, as shown below.

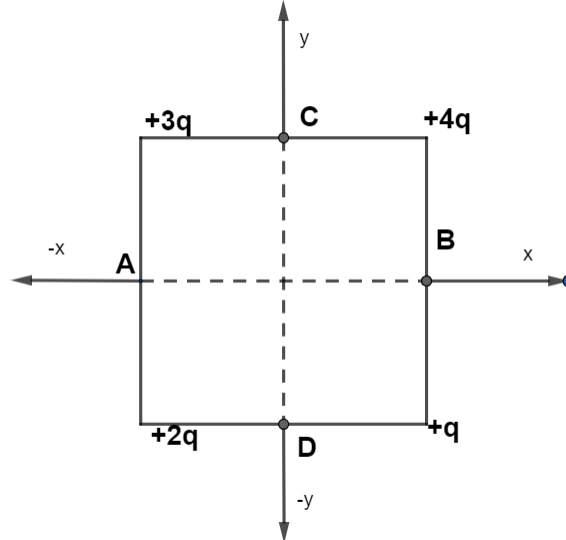
Imagine a unit positive test charge at the centre of the square. As the shape is a square so the distance of each charge from the central charge is the same, let it be a.
Now,

Force acting at test Charge Q, due to +q, ${F_{ + q}} = k\dfrac{{qQ}}{{{a^2}}}\left( {a\hat i - a\hat j} \right)$
Force acting at test Charge Q, due to +3q, ${F_{ + 3q}} = k\dfrac{{3qQ}}{{{a^2}}}\left( { - a\hat i + a\hat j} \right)$
Force acting at test Charge Q, due to +2q, ${F_{ + 2q}} = k\dfrac{{2qQ}}{{{a^2}}}\left( { - a\hat i - a\hat j} \right)$
Force acting at test Charge Q, due to +4q, ${F_{ + 4q}} = k\dfrac{{4qQ}}{{{a^2}}}\left( {a\hat i - a\hat j} \right)$
Clearly, the distance is the same for all the charges. Thus the resultant force only depends upon the magnitude of the charges.

Thus the net force acting at the unit positive test charge Q, is $4a\hat j$
The following diagram shows the respective direction of all the electric fields acting at the center with blue coloured paths. Similarly, the resultant force acting along DC is represented by a green coloured path.

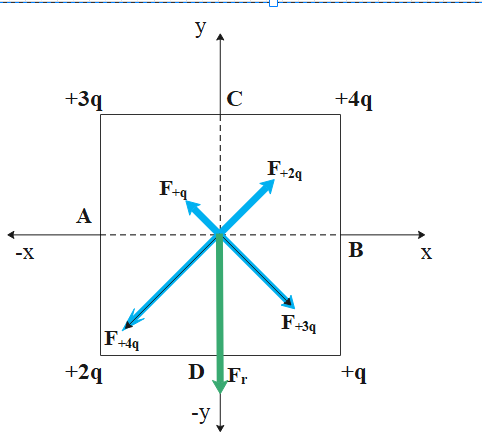
Therefore the direction of electric field at the center of the given square is along DC.

Note : The electric field lines are used to represent the direction of electric fields, which are imaginary lines in nature. The electric field lines from a unit positive charge are directed radially outwards extending to infinity in spherical shape. Similar to electric field lines of a positive point charge, the negative charge is also spherical but inwards in direction.