Question

Four charges $2C$ , $- 3C$ , $- 4C$ and $5C$ respectively are placed at the four corners of a square. Which of the following statements is true for the point of intersection of the diagonals?
A. $E = 0,V = 0$
B. $E \ne 0,V = 0$
C. $E = 0,V \ne 0$
D. $E \ne 0,V \ne 0$

Answer 1

Electric potential due to a point charge is calculated as $V = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{Q}{r}$ which is a scalar quantity and net electric potential due to multiple charges can be added by using scalar addition. Electric field due to a point charge is $E = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{Q}{{{r^2}}}$ which a vector quantity is.

Complete step by step answer:
Let us draw the diagram of a given problem as, let $P$ be the point at the centre.

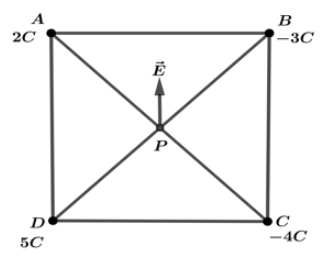
Intersection of diagonals of square and let $L$ be the distance from each charge to the point $P$ such that $AP = BP = CP = DP = L$. Now, we will find the electric potential at point $P$ due to each charge one by one. Electric potential due to $2C$ be given by
${V_A} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{2}{L}$ Joules per coulomb
Electric potential due to $- 3C$ be given by,
${V_B} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{ - 3}}{L}$ Joules per coulomb
Electric potential due to $- 4C$ be given by,
${V_C} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{ - 4}}{L}$ Joules per coulomb
Electric potential due to $5C$ be given by,
${V_D} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{5}{L}$ Joules per coulomb
Now, adding all four potentials, we will get net potential at point $P$
${V_P} =$ $\dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{1}{L}(5 + 2 - 3 - 4)$
$\therefore {V_P} =$ $0$
Hence potential at the point of intersection of diagonal is zero. As we know, an electric field is a vector quantity and their resultant is always added using vector algebra which shows at the point of intersection of diagonals the electric field cannot be zero. So, we get $E \ne 0,V = 0$

Hence, the correct option is B.

Note: Here, $\dfrac{1}{{4\pi {\varepsilon _0}}}$ is also denoted as $k$ which is a proportionality constant which has a numerical value of $9 \times {10^9}N{m^2}{C^{ - 2}}$ and the ${\varepsilon _0}$ is called the permittivity of free space. Electric field is a vector quantity whose direction due to positive charge is always away from the point charge and for negative charge it’s towards the point charge.