Question
Question: Four capacitors \({C_1}\), \({C_2}\), \({C_3}\), \({C_4}\) are connected as shown in figure below. C...
Four capacitors C1, C2, C3, C4 are connected as shown in figure below. Calculate the equivalent capacitance of the circuit between points X and Y.
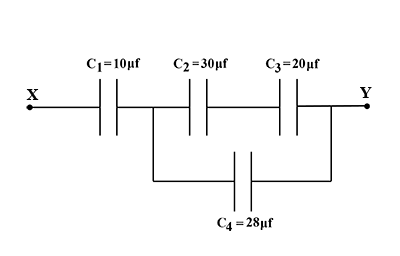
Solution
Use the formula for equivalent capacitance when the capacitors are connected in series and parallel. Remember that in a set of parallel capacitors the total capacitance is just a sum of the individual capacitors and in the series capacitance, the reciprocal sum of the individual capacitors gives the total capacitance.
Formula used:
C′11=C21+C31
Where C1′,C2,C3 are capacitance of the capacitance.
Complete step by step answer:
We know that,
⇒C′11=C21+C31
Therefore,
⇒C′11=201+301
Therefore,
⇒C1′=12μF
Since the capacitors C1′ and C4 are connected in series,
⇒C1’’=12+28
⇒C1‘’=40μF
From this we can calculate,
⇒C1=101+401
⇒404+1
⇒C1=405
∴81
Therefore,
C=8μF
Thus, we can conclude that the equivalent capacitance of the circuit between points X and Y is 8 F.
Additional information:
Capacitors can also be called electric condensers. It is an electrical component with two terminals, that can store energy in the form of electrical charge. Capacitors are usually used to increase the effects of capacitance. Capacitance is a proportional constant that relates charge to the potential difference between two conductors. It is used to measure in the units of Farad.
We know,
Q=VC
Where C=capacitance, Q= charge contained in the capacitor, V= potential difference between two conductors.
Usually, most capacitors have two electrical conductors separated by a metallic plate, also known as the dielectric medium. Most capacitors are used in appliances that require sudden huge bursts of energy, like fans, air conditioners, mobile phones. A capacitor is always required to be placed in a power circuit with a given applied voltage of either alternating or direct current. Capacitors are used to separate the A.C and D.C, to filter out the unwanted signals, used as a sensing device and used in the audio system of the vehicle.
Note:
If the capacitors, C1, C2 are connected in series, the equivalent capacitance is given by C1=C11+C21.... On the other hand, if the capacitors, C1, C2 are connected in parallel then the equivalent capacitance is given by C=C1+C2...
