Question

Four capacitors and a switch S are connected to a source as shown in the figure. Initially S is open and the capacitors are uncharged. After S is closed and steady state is reached. What is the energy stored in the $4\mu F$ capacitor in the units of ${{10}^{-5}}J$ ?

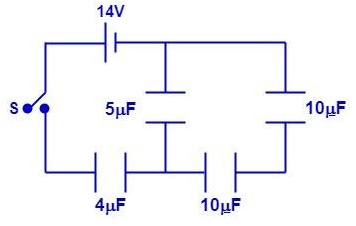
(A) 40
(B) 30
(C) 20
(D) 15

Answer 1

Resolve all the combination of capacitors using capacitors in series and parallel formula i.e.
$\begin{aligned} & {{\text{C}}_{\text{p}}}={{\text{C}}_{1}}+{{\text{C}}_{2}}+..........{{\text{C}}_{\text{n}}} \\\ & \dfrac{1}{{{\text{C}}_{s}}}=\dfrac{1}{{{\text{C}}_{1}}}+\dfrac{1}{{{\text{C}}_{2}}}+......\dfrac{1}{{{\text{C}}_{\text{n}}}} \\\ \end{aligned}$
Then calculate the charge in the circuit. As charge remains the same in series combination so charge in the $\text{4 }\\!\\!\mu\\!\\!\text{ f}$ capacitor is the same as that in the whole circuit. Using the formula of energy, we can get the required answer.
$\text{U}=\dfrac{{{\text{Q}}^{2}}}{2\text{C}}$

Complete step by step solution

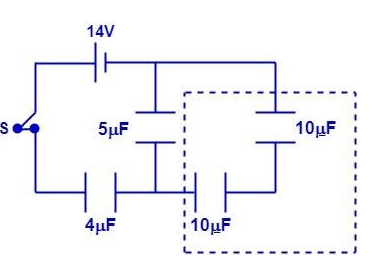
When the switch is closed and the steady state is reached, the charge in the circuit is fixed.
First we resolve the combinations of capacitors.
We can see that the two capacitors of $\text{10 }\\!\\!\mu\\!\\!\text{ f}$ are in series with each other so their resultant capacitance is:
$\begin{aligned} & \dfrac{1}{{{\text{C}}_{1}}}=\dfrac{1}{10}+\dfrac{1}{10}=\dfrac{10+10}{100} \\\ & {{\text{C}}_{1}}=\dfrac{100}{20}=5\text{ }\\!\\!\mu\\!\\!\text{ f} \\\ \end{aligned}$

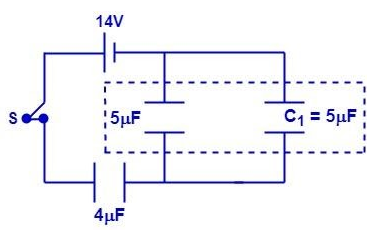
Now both ${{\text{C}}_{1}}=5\text{ }\\!\\!\mu\\!\\!\text{ f}$ and the other $5\text{ }\\!\\!\mu\\!\\!\text{ f}$ capacitor are in parallel so the resultant capacitance will be
$\begin{aligned} & {{\text{C}}_{2}}={{\text{C}}_{1}}+5 \\\ & =5+5 \\\ & =10\text{ }\\!\\!\mu\\!\\!\text{ f} \\\ \end{aligned}$
Now the circuit formed is

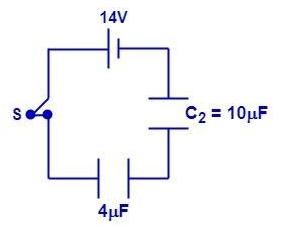
Now applying the Kirchhoff’s voltage law in the formed circuit
We get,
$\begin{aligned} & 14-\dfrac{\text{Q}}{10\times {{10}^{-6}}}-\dfrac{\text{Q}}{4\times {{10}^{-6}}}=0 \\\ & \dfrac{280\times {{10}^{-6}}-2\text{Q}-5\text{Q}}{20\times {{10}^{-6}}}=0 \\\ & 280\times {{10}^{-6}}-7\text{Q=0} \\\ & \text{280}\times {{10}^{-6}}=7\text{Q} \\\ & \text{Q}=\dfrac{280}{7}\times {{10}^{-6}} \\\ & =40\times {{10}^{-6}}\text{C} \\\ & \text{=40 }\\!\\!\mu\\!\\!\text{ C} \\\ \end{aligned}$
Energy in $\text{4 }\\!\\!\mu\\!\\!\text{ f}$ capacitor $=\dfrac{{{\text{Q}}^{2}}}{2\text{C}}$
$\begin{aligned} & \text{U}=\dfrac{{{\left( 40\times {{10}^{-6}} \right)}^{2}}}{2\times 4\times {{10}^{-6}}} \\\ & \text{ =}\dfrac{1600\times {{10}^{-12}}}{8\times {{10}^{-6}}} \\\ & \text{U}=200\times {{10}^{-6}}\text{ J} \\\ & \text{U}=20\times {{10}^{-5}}\text{ J} \\\ \end{aligned}$
Therefore the correct option is (C).

Note
Always resolve all the capacitors into the simplest circuit first while solving these kinds of questions.
Also we can calculate the charge Q in the capacitor without applying Kirchhoff law by using the formula
Q = CV
V = 14V
Where C is the net capacitance in the whole circuit. This can be calculated as ${{\text{C}}_{2}}=10\text{ }\\!\\!\mu\\!\\!\text{ f}$ and $\text{4 }\\!\\!\mu\\!\\!\text{ f}$ capacitors are in series combination.
So
$\begin{aligned} & \dfrac{1}{\text{C}}=\dfrac{1}{{{\text{C}}_{2}}}+\dfrac{1}{4\times {{10}^{-6}}}=\left[ \dfrac{1}{10}+\dfrac{1}{4} \right]\times {{10}^{6}} \\\ & \dfrac{1}{\text{C}}=\left[ \dfrac{2+50}{20} \right]\times {{10}^{6}} \\\ & \text{C}=\dfrac{20}{7}\times {{10}^{-6}} \\\ & =\dfrac{20}{7}\text{ }\\!\\!\mu\\!\\!\text{ f} \\\ \end{aligned}$
So
$\begin{aligned} & \text{Q}=\dfrac{20}{7}\times {{10}^{-6}}\times 14 \\\ & \text{ }=40\times {{10}^{-6}}\text{ C} \\\ & \text{Q}=40\text{ }\\!\\!\mu\\!\\!\text{ C} \\\ \end{aligned}$
From this value of charge we get the value of energy in the given capacitor.