Question

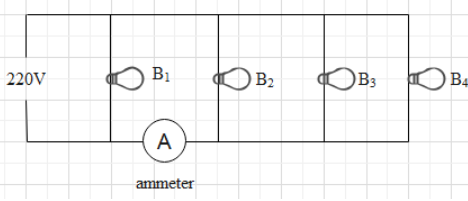
Four bulbs ${{B}_{1}},{{B}_{2}},{{B}_{3}}$ and ${{B}_{4}}$ of 100 W each are connected to 220 V mains as shown in the figure. The reading in an ideal ammeter will be:

A. 0.45A
B. 0.90A
C. 1.35A
D. 1.80A

Answer 1

To solve this question, first from the given power and the voltage, find the current passing through each of the bulbs. From the circuit diagram observe the position of the ammeter and find the bulbs, the current through which will also pass through the ammeter. Then find the total current passing through the ammeter.

Complete answer:
Given in the question that, the power of each bulb is $P=100W$
The bulbs are connected to a voltage source, $V=220V$
Electric power can be mathematically expressed as the product of the voltage and current through the circuit.
$P=VI$
Where, V is the voltage and I is the current through the circuit.
So, electric current can be expressed in terms of power and voltage as,
$I=\dfrac{P}{V}$
Electric current passing through each bulb will be,
$I=\dfrac{100W}{220V}=\dfrac{5}{11}A$
Now, from the circuit diagram, we know that the ammeter will read the current only through the bulbs ${{B}_{2}},{{B}_{3}},{{B}_{4}}$.
So, the total current passing through the ammeter will be,
$\begin{aligned} & I=3\times \dfrac{5}{11}A \\\ & I=1.35A \\\ \end{aligned}$
So, the reading in the ammeter will be 1.35A

The correct option will be (C).

Note:
Electrical power can be defined as the measure of the rate of electrical energy transferred by an electric circuit per unit time. The SI unit of electric power is watt or joule per second. The formula for electric power is
$P=VI$
Again, from Ohm’s law we can write that,
$V=IR$
Where, R is the resistance of the material or the circuit through which the current is passed.
Putting this on the above equation we can also express power mathematically as,
$\begin{aligned} & P={{I}^{2}}R \\\ & P=\dfrac{{{V}^{2}}}{R} \\\ \end{aligned}$