Question
Question: Four blocks and two springs are connected as shown in the figure. The system is at rest, determining...
Four blocks and two springs are connected as shown in the figure. The system is at rest, determining the acceleration of all the loads immediately after the lower thread keeping the system in equilibrium has been cut. Assume that the threads are weightless, the mass of the pulley is negligibly small, and there is no friction at the point of suspension.
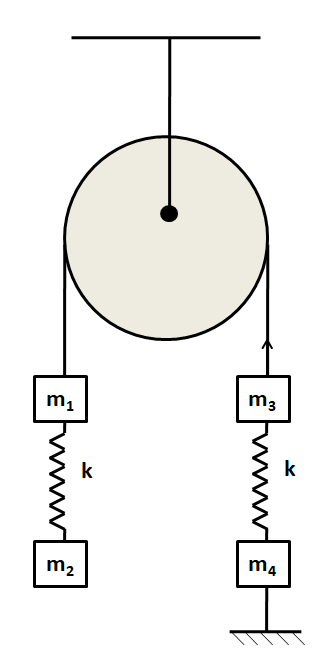
Solution
To solve this question, we need to find out the forces in the springs and the strings from the equilibrium of the four blocks. After the lower thread is cut, these values will remain unchanged, so applying Newton's second law of motion, we can get the accelerations of all the blocks.
Complete step by step solution:
Let the tension in the string be T
Also, let the forces in the left and the right springs be F1 and F2 respectively.
Now, if the lower thread is keeping the system in equilibrium, so the blocks at the right must be pulled up by the blocks at the right. For that, we must have
⇒m1+m2>m3+m4
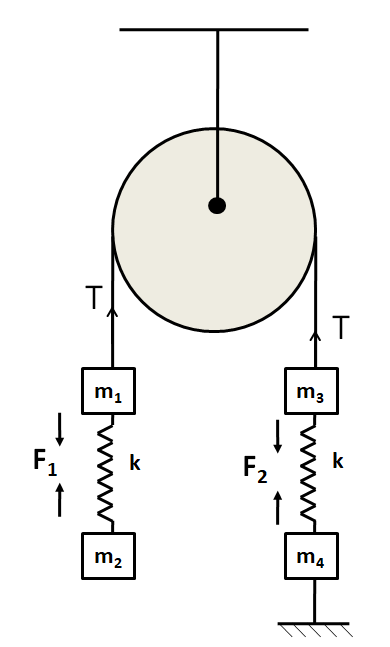
From the equilibrium of the mass m2 we have
⇒F1=m2g (i)
From the equilibrium of the mass m1 we have
⇒T=F1+m1g
From (i)
⇒T=m2g+m1g
⇒T=(m1+m2)g (ii)
From the equilibrium of the mass m3
⇒F2+m3g=T
From (ii)
⇒F2+m3g=(m1+m2)g
⇒F2=(m1+m2−m3)g (iii)
Now, when the lower thread is cut, let the acceleration of the blocks of massesm1, m2, m3, and m4 be a1 a2, a3, anda4respectively.
At the instant of cutting the lower thread, the extensions of the springs remain the same, and hence the forces in them will remain the same. So, F1 and F2 will be the same as calculated above.
Also since m1+m2>m3+m4, so the blocks on the left will come downward and the blocks at the right will come upwards. Therefore, the directions of the accelerations are shown as
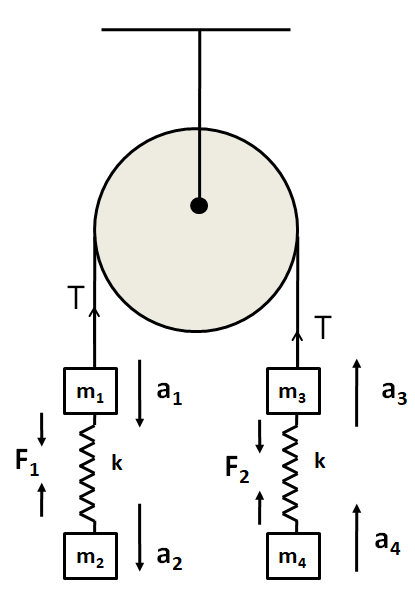
Now, we apply the Newton’s second law of motion on each of the blocks
For the block m2
⇒m2g−F1=m2a2
From (i)
⇒m2g−m2g=m2a2
⇒m2a2=0
Since the mass m2 is not zero, so we have
⇒a2=0
For the block m1
⇒m1g+F1−T=m1a1
From (i) and (ii)
⇒m1g+m2g−(m1+m2)g=m1a1
⇒m1a1=0
Since the massm1is not zero, so we have
⇒a1=0
For the block m3
⇒T−m3g−F2=m3a3
From (ii) and (iii)
⇒(m1+m2)g−m3g−(m1+m2−m3)g=m3a3
⇒(m1+m2)g−m3g−(m1+m2)g+m3g=m3a3
On simplifying, we get
⇒m3a3=0
Since the mass m3 is not zero, so we have
⇒a3=0
For the block m4
⇒F2−m4g=m4a4
From (iii)
⇒(m1+m2−m3)g−m4g=m4a4
⇒(m1+m2−m3−m4)g=m4a4
Dividing bym4we get
⇒a4=m4(m1+m2−m3−m4)g
Hence, the accelerations of the blocks immediately after the lower thread is cut are
⇒a1=a2=a3=0 and a4=m4(m1+m2−m3−m4)g.
Note:
There is no need to consider the tension in the lower thread and find out the value of the tension in it. Although we can find it out, it is of no use in our calculations. As we have to make all the calculations after the thread is cut, so its tension becomes zero at the instant. The tension provided by the thread before being cut is just keeping the blocks in the equilibrium.
