Question
Question: Four blocks \( A,B,C,D \) with masses \( 1kg,2kg,3kg,4kg \) respectively are connected as shown in t...
Four blocks A,B,C,D with masses 1kg,2kg,3kg,4kg respectively are connected as shown in the figure. If system is released from rest, then tension in the string connecting blocks A and C is –
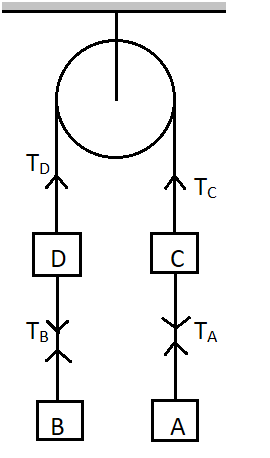
Solution
Hint : Tension Force is a type of ‘pull’ force which acts on an object tied to a string and its acts because of the string. In cases like this, the complete system is assumed to be an isolated system, that is no external force acts on the said system.
Complete Step By Step Answer:
Tension is a kind of force which acts on a body which is tied to a string and its direction is always away from the body. Which means that tension is a type of ‘pull’ force.
When in an isolated system, the forces that we need to consider are the forces already acting on its components and their weights. After considering these forces we need to find out the net force acting on the system and the acceleration by which its components will move.
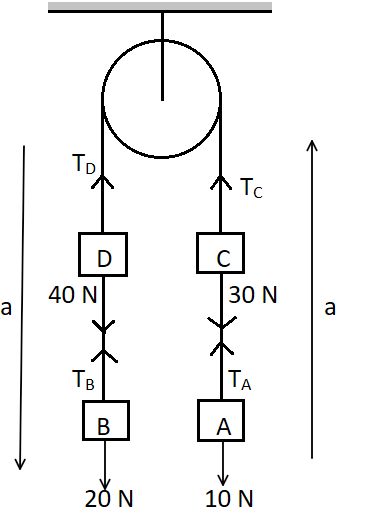
So the net force acting on the system is,
Fnet=∣(20N+40N)−(10N+30N)∣
Fnet=60N−40N
Fnet=20N
Also,
Fnet=Ma
Where, M= total mass of the components
a= Net acceleration
20N=(1+2+3+4)×a
a=1020
a=2ms−2
So, each component moves with the acceleration of 2ms−2 . The direction however differs. Blocks A and C move in upwards direction, whereas blocks B and D move in downward direction.
Now to calculate the tension in the string connecting blocks A and C (TA) , we make a free body diagram of block A .
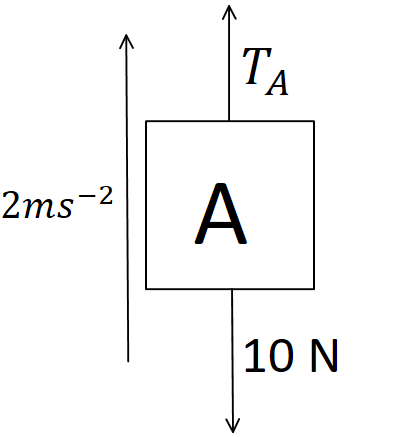
So in this case,
Fnet=mAa
⇒TA−10=1×2
⇒TA−10=2
∴TA=12N
Thus, tension in the string connecting blocks A and C is 12N .
Note :
In this case, when the mass of string is not given, the string is to be considered massless. If the mass of string is given, it changes the whole dynamic of the system since its weight is also to be taken into account. The pulleys by which the strings are connected are also considered frictionless, otherwise whole other problems emerge.
