Question

Forces proportional to ${\text{AB}}$, ${\text{BC}}$ and ${\text{2CA}}$ act along the sides of triangle ${\text{ABC}}$ in order. Their resultant represented in magnitude and direction as
A. $\overrightarrow {{\text{CA}}}$
B. $\overrightarrow {{\text{AC}}}$
C. $\overrightarrow {{\text{BC}}}$
D. $\overrightarrow {{\text{CB}}}$

Answer 1

We are asked to find the resultant of three vectors $\overrightarrow {{\text{AB}}}$, $\overrightarrow {{\text{BC}}}$ and ${\text{2}}\overrightarrow {{\text{CA}}}$ along three sides of the triangle ABC. First, find the resultant of vectors $\overrightarrow {{\text{AB}}}$ and $\overrightarrow {{\text{BC}}}$, for this you will need to use triangle law of vectors. Using this law find the resultant of vectors $\overrightarrow {{\text{AB}}}$ and $\overrightarrow {{\text{BC}}}$ and then we with vector obtained find its resultant with vector ${\text{2}}\overrightarrow {{\text{CA}}}$.

Complete step by step answer:
Given, the forces proportional to ${\text{AB}}$, ${\text{BC}}$ and ${\text{2CA}}$ act along the sides of triangle ${\text{ABC}}$ in order.Let the force acting along the side ${\text{AB}}$ be $\overrightarrow {{\text{AB}}}$, the force acting along the side ${\text{BC}}$ be $\overrightarrow {{\text{BC}}}$ and the force acting along the side ${\text{AC}}$ be $\overrightarrow {{\text{AC}}}$.The force ${\text{2}}\overrightarrow {{\text{CA}}}$ will act opposite to force $\overrightarrow {{\text{AC}}}$.

Let us draw a diagram for the problem.

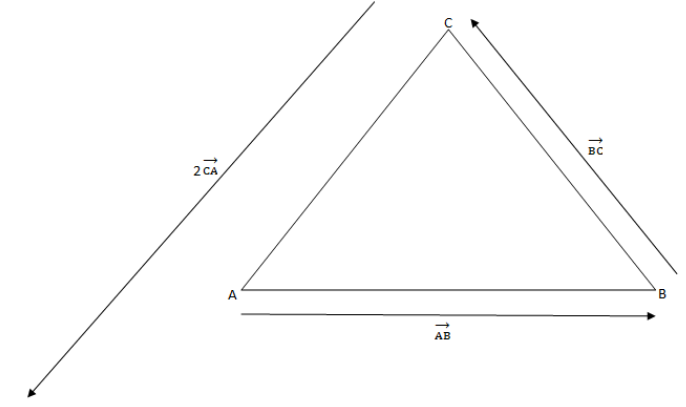
To find the resultant vector of $\overrightarrow {{\text{AB}}}$ and $\overrightarrow {{\text{BC}}}$ , we will use the triangle law of vectors, according to which if two vectors represents two sides of a triangle with their magnitude and direction then the resultant of the two vectors is represented by the third side of the triangle.Here, $\overrightarrow {{\text{AB}}}$ and $\overrightarrow {{\text{BC}}}$ are two vectors along two sides of triangle ABC so the resultant vector will be along the side ${\text{AC}}$ that will be $\overrightarrow {{\text{AC}}}$.

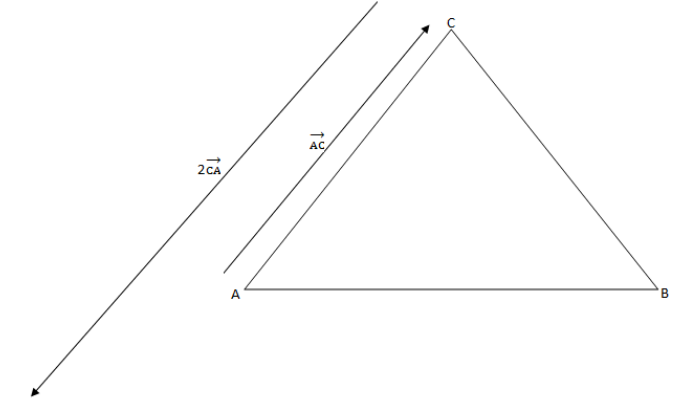
Now, the resultant of vector ${\text{2}}\overrightarrow {{\text{CA}}}$ and $\overrightarrow {{\text{AC}}}$ will be,
$\overrightarrow {\text{R}} = {\text{2}}\overrightarrow {{\text{CA}}} + \overrightarrow {{\text{AC}}}$
The vector $\overrightarrow {{\text{AC}}}$ can be written as $\left( { - \overrightarrow {{\text{CA}}} } \right)$. Substituting this value in the above equation we get,
$\overrightarrow {\text{R}} = {\text{2}}\overrightarrow {{\text{CA}}} - \overrightarrow {{\text{CA}}}$
$\therefore \overrightarrow {\text{R}} = \overrightarrow {{\text{CA}}}$
Therefore, the resultant vector is $\overrightarrow {{\text{CA}}}$ with magnitude ${\text{CA}}$ and direction from point C to point A.

Hence, the correct answer is option A.

Note: A vector is a quantity which has both magnitude and direction. There are two important laws of vector addition which are triangle law and parallelogram of vector addition. In the above question we have discussed triangle law of vector addition.Parallelogram law of vector addition states that if two vectors represent two adjacent sides of a parallelogram then the diagonal from the common point of the two adjacent sides represents the resultant or sum of the two vectors.