Question

Force versus Elongation graph of a wire is shown in the figure for two different temperatures ${T_1}$ and ${T_2}$ , then,

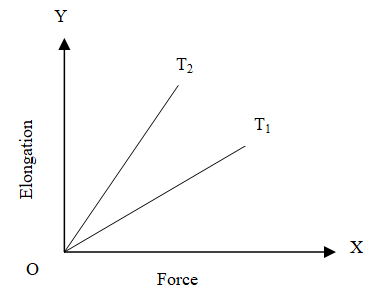
(A) ${T_1} = {T_2}$
(B) ${T_1} < {T_2}$
(C) ${T_1} > {T_2}$
(D) Cannot be predicted.

Answer 1

Hint To solve this question, we have to use the relationship between Young’s modulus of a metal and the temperature. Using it, we can easily determine the relationship between temperatures ${T_1}$ and ${T_2}$ .
Formula Used: The formulae used to solve this question are given by:
$Y = \dfrac{\sigma }{\tau }$
Here $Y$ is the Young’s Modulus of the wire, $\sigma$ is the stress, and $\tau$ is the longitudinal strain.
$\sigma = \dfrac{F}{A}$
$\tau = \dfrac{{\delta l}}{L}$
Here, $F$ is the force acting on the wire, $A$ is the area of cross-section of the wire perpendicular to which the force is acting, $\delta l$ is the elongation of the wire, and $L$ is the length of the wire.

Complete step by step answer
Let us first calculate the slope of the given graph. This gives us,
$slope = \dfrac{{\Delta Y}}{{\Delta X}}$
Since $Y$ is the elongation and $X$ is the force, so we get the slope as,
$slope = \dfrac{{\delta l}}{F}$
Now, we know Young’s Modulus is given as,
$Y = \dfrac{\sigma }{\tau }$
So, putting in the values of $\sigma$ and $\tau$ in $Y$ we get,
$Y = \dfrac{{\dfrac{F}{A}}}{{\dfrac{{\delta l}}{L}}} \\\ \Rightarrow Y = \dfrac{{F.L}}{{A.\delta l}} \\\$
So, rearranging the terms, we can write,
$Y = \dfrac{L}{A}.\left( {\dfrac{F}{{\delta l}}} \right)$
But, from the slope we calculated, we know that,
$\dfrac{F}{{\delta l}} = \dfrac{1}{{slope}}$
So, we get Young’s Modulus as,
$Y = \dfrac{L}{A}.\left( {\dfrac{1}{{slope}}} \right)$
This means, that Young’s Modulus is inversely proportional to the slope of the graph, i.e.
$Y \propto \dfrac{1}{{slope}}$
Since slope of line representing ${T_2}$ is greater than slope of line representing ${T_1}$ , so,
${Y_1} > {Y_2}$
Here ${Y_1}$ is the Young’s modulus of line representing ${T_1}$ and ${Y_2}$ is the Young’s modulus of line representing ${T_2}$ .
Now, an important concept to understand here is the variation of Young’s modulus with temperature. We should understand that when we increase the temperature of the wire, it increases the vibration of atoms in the crystal structure of the metal that makes the wire. These vibrations cause an increase in the atomic distance between two neighboring atoms and thus decrease the atomic force binding them. This leads to a decrease in the Young’s modulus of the material of the wire, as now less stress is required to mould or break the wire.
Hence, we can say that, Young’s modulus is inversely proportional to temperature, i.e.
$Y \propto \dfrac{1}{T}$
Now since we found that,
${Y_1} > {Y_2}$
So, we get,
${T_2} > {T_1}$
$\therefore$ Option (B) is the correct option.

Note
We should note that here we have considered the material of the wire to be a metal. For different materials other than metals, the relationship between Young’s modulus and Temperature would differ.