Question

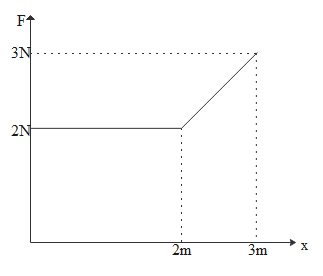
Force versus displacement graph of a particle starting from rest is given in the figure shown. The kinetic energy of particle at x=3m is:

A. $6.5J$
B. $7.5J$
C. $6J$
D. $5J$

Answer 1

Whenever these kinds of questions are given we should check the variables on x and y axes, and what was asked. Here the variables are force and displacement and we were asked to find out kinetic energy. Hence the equation relating force, displacement and kinetic energy must be used and graphs should be interpreted accordingly to solve it.

Formula used:
$W = F.x = \Delta KE$

Complete step-by-step answer:
The units of kinetic energy are joules. The units of work done are also joules. The relation between kinetic energy and work done can be understood by the work-energy theorem.
Work energy theorem states that work done by all the forces combined will result in change in kinetic energy $W = F.x = \Delta KE$
Where ‘W’ is work done by all the forces and ‘x’ is displacement and ‘F’ is the force and $\Delta KE$ is change in kinetic energy.
The plot given is between force and displacement. Hence if we find the area under that graph, we can get the work done and it will be equal to change in kinetic energy.

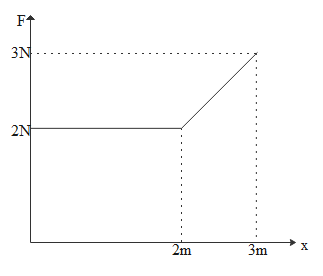
Area of the square having 2m as length and 2N as breadth is
${A_1} = 2 \times 2 = 4$
Area of rectangle having $3 - 2 = 1m$ as length and 2N as breadth is
${A_2} = 1 \times 2 = 2$
Area of triangle having $3 - 2 = 1m$ as base and $3 - 2 = 1N$as height is
${A_3} = \dfrac{1}{2} \times 1 \times 1 = \dfrac{1}{2}$
So total area is
\eqalign{ & {A_1} + {A_2} + {A_3} \cr & \Rightarrow 4 + 2 + \dfrac{1}{2} \cr & \Rightarrow 4 + 2 + 0.5 \cr & \Rightarrow 6.5J \cr}
Initial kinetic energy is zero as it started from the rest, so final kinetic energy i.e kinetic energy at 3m position is 6.5 joules.

So, the correct answer is “Option A”.

Note: In the work energy theorem, work done by all the forces includes all kinds of forces i.e they might be conservative or non conservative or external. This work energy theorem is the basis for conservation of the mechanical energy equation when no non conservative forces are present.