Question

Force on current carrying loop (Radius=R) in uniform magnetic (B) field which is at an angle $30{}^\circ$ with the normal will be
A. Zero
B. $2\pi RiB$
C. $2\sqrt{3}\pi iB$
D. $\pi iB$

Answer 1

We have a current carrying loop of radius R in a uniform magnetic field. The angle between the normal and the magnetic field is given to us. We know that a current carrying loop will only experience a torque in a uniform magnetic field.

Complete step by step answer:
In the question we are given a current carrying loop of radius R in a uniform magnetic field. The strength of the magnetic field is given as B. the angle between the field and the normal is given as $30{}^\circ$.
The figure below shows a current carrying loop as said in the question.

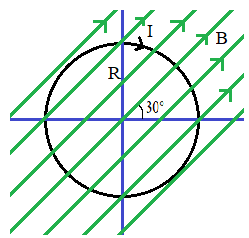
Here we have a uniform magnetic field and a current carrying loop.
We know that a current carrying loop in a uniform magnetic field will only experience torque, i.e. it will not have any force.
Therefore we can say that a current carrying loop in a uniform magnetic field will have a force which is equal to zero.
$\therefore Force=0$
Hence the correct answer is option A.

Note:
As said before, a current carrying loop in a uniform magnetic field will experience a torque.
The equation for torque on a current carrying loop in uniform magnetic field is given as,
$\tau =\vec{\mu }\times \vec{B}$, were ‘$\mu$’ is the magnetic moment and ‘B’ is the magnetic field.
$\Rightarrow \tau =\vec{\mu }\vec{B}\sin \theta$
Magnetic moment can be found using the equation,
$\mu =IA$, were ‘I’ is the current and ‘A’ is the area.
Since ‘R’ is the radius of the loop, we will get the area of the loop as,
$A=\pi {{R}^{2}}$
Therefore we get the magnetic moment as,
$\therefore \mu =\pi {{R}^{2}}I$
Therefore, by substituting this, the equation for torque will become,
$\therefore \tau =\left( \pi {{R}^{2}}I \right)\vec{B}\sin \theta$
From the question we have $\theta =30{}^\circ$
$\therefore \tau =\left( \pi {{R}^{2}}I \right)\vec{B}\sin 30$
$\Rightarrow \tau =\left( \pi {{R}^{2}}I \right)\vec{B}\times \dfrac{1}{2}$
$\therefore \tau =\dfrac{\pi }{2}\vec{B}{{R}^{2}}I$
This is the equation for torque of a current carrying loop in a uniform magnetic field.