Solveeit Logo
Login

Question

Question: Force between two plates of a capacitor is: A). \(\dfrac{Q}{{{\varepsilon _0}A}}\) B). \(\dfrac{...

Force between two plates of a capacitor is:
A). Qε0A\dfrac{Q}{{{\varepsilon _0}A}}
B). Q22ε0A\dfrac{{{Q^2}}}{{2{\varepsilon _0}A}}
C). Q2ε0A\dfrac{{{Q^2}}}{{{\varepsilon _0}A}}
D). None of these

Explanation

Solution

In order to deal with this question we will apply the general equation of force in physics, so for it first we will write the magnitude of the electric field by anyone plate. Use the concept of electrostatics in order to solve the problem.

Formula used: E=σ2ε0,σ=QA,∣F∣=∣Q∣⋅∣E∣E = \dfrac{\sigma }{{2{\varepsilon _0}}},\sigma = \dfrac{Q}{A},\left| F \right| = \left| Q \right| \cdot \left| E \right| where E = Electric Field , σ\sigma = area density of charge , ε0{\varepsilon _0}= vacuum permittivity ,Q= total charge on a plate ,A= area of each plate ,F= Force between two plates.

Complete step-by-step solution:
__

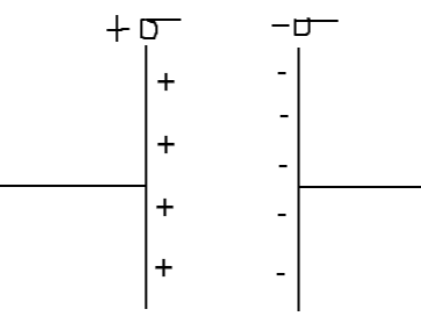
We know that the magnitude of the electric field by anyone plate is given as
E=σ2ε0E = \dfrac{\sigma }{{2{\varepsilon _0}}}
And we know that , σ=QA\sigma = \dfrac{Q}{A}
∴E=σ2ε0=Q2Aε0\therefore E = \dfrac{\sigma }{{2{\varepsilon _0}}} = \dfrac{Q}{{2A{\varepsilon _0}}}
Now , the magnitude of the force between the two plates of the capacitor can be found as:
∣F∣=∣Q∣⋅∣E∣\left| F \right| = \left| Q \right| \cdot \left| E \right|
Substituting the value of electric field (E) , we will get
∣F∣=∣Q∣⋅∣E∣ ⇒F=Q⋅Q2Aε0 ⇒F=Q22Aε0  \left| F \right| = \left| Q \right| \cdot \left| E \right| \\\ \Rightarrow F = Q \cdot \dfrac{Q}{{2A{\varepsilon _0}}} \\\ \Rightarrow F = \dfrac{{{Q^2}}}{{2A{\varepsilon _0}}} \\\
Hence, the force between two plates of a capacitor is Q22Aε0\dfrac{{{Q^2}}}{{2A{\varepsilon _0}}}
So, the correct answer is option B.

Note: When two parallel plates are connected across a battery, the plates are charged and an electric field is established between them, and this setup is known as the parallel plate capacitor. A parallel plate capacitor behaves as open-circuited when we connect a DC source across it, while it acts as a short circuit when we connect an AC source to it. The said property of a parallel plate capacitor makes it suitable for filtering the harmonics from the AC supply.