Question

For ƒ(x) = x² – 2 |x|, test the continuity and differentiability of g(x) in the interval [-2, 3], where

g (x) =$f(x) = \left| \begin{matrix} \sin x & \cos x & \tan x \\ x^{3} & x^{2} & x \\ 2x & 1 & 1 \end{matrix} \right|$, are –

• A. g (x) is continuous and differentiable everywhere except x = 0
• B. g (x) is non-differentiable at x = 0 and 2
• C. g (x) is non-differentiable at x = 0, 1, 2
• D. None of the above

Answer 1

Answer: (B)

g (x) is non-differentiable at x = 0 and 2

Answer 2

1. (2)

Sol. Here ƒ(x) = $\left\{ \begin{array} { c c } \mathrm { x } ^ { 2 } + 2 \mathrm { x } , & \mathrm { x } < 0 \\ 0 , & \mathrm { x } = 0 \\ \mathrm { x } ^ { 2 } - 2 \mathrm { x } , & \mathrm { x } > 0 \end{array} \right.$

Case 1 : –2 ≤ x < –1, ƒ(x) decreases ⇒ g (x) = x² + 2x

Case 2 : –1 ≤ x < 0, ƒ(x) increases ⇒ g (x) = –1

Case 3 : 0 ≤ x < 1, ƒ(x) decreases ⇒ g(x) = 0

Case 4 : 1 ≤ x < 2, ƒ(x) increases but ƒ(x) < 0

⇒ g (x) = ƒ(0) = 0

Case 5 : 2 ≤ x ≤ 3, ƒ(x) increases and ƒ(x) ≥ 0

∀ x ∈ [2, 3)

⇒ g (x) = ƒ (x) = x² – 2x, 2 ≤ x ≤ 3

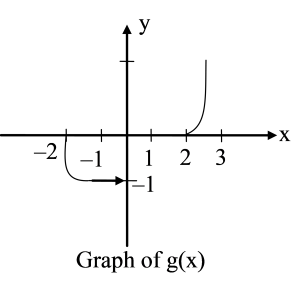
Therefore g (x) =

Clearly g (x) is continuous everywhere except at x = 0.

Also g (x) is non differentiable at x = 0 and 2.

Hence (2) is the correct answer.