Question

For what value of k, $\left( 4-k \right){{x}^{2}}+2\left( k+2 \right)x+\left( 8k+1 \right)$ is a perfect square.
$\left( a \right)k=3$
$\left( b \right)k=0$
(c) does not exist
(d) Both (a) and (b)

Answer 1

To solve this question, observe the quadratic equation given as $a{{x}^{2}}+bx+c=0$ where this equation has 2 equal roots, then its discriminant $D={{b}^{2}}-4ac$ becomes equal to zero. We will use this concept to solve this question. When the value of the given equation is a perfect square, the roots are equal, so we get, $D={{b}^{2}}-4ac=0.$

Complete step-by-step solution
We are given the value $\left( 4-k \right){{x}^{2}}+2\left( k+2 \right)x+\left( 8k+1 \right)$ is a perfect square. This above given is a quadratic equation. A quadratic equation is of order 2. It has two roots, therefore the above-given equation being quadratic has 2 roots.
$\Rightarrow \left( 4-k \right){{x}^{2}}+2\left( k+2 \right)x+\left( 8k+1 \right)$ has 2 roots.
We are given that this equation is a perfect square. So, both the roots are equal as then only they can form ${{a}^{'}}\times {{a}^{'}}={{\left( {{a}^{'}} \right)}^{2}}$ where a is the root (assumed). When our equation is given of the form, $a{{x}^{2}}+bx+c=0$ and the roots are equal.
$\Rightarrow \Delta =D={{b}^{2}}-4ac=0$
That is, their discriminant is equal to zero.
Comparing our equation from $a{{x}^{2}}+bx+c=0,$ we get,
$a=\left( 4-k \right)$
$b=2\left( k+2 \right)$
$c=8k+1$
Using $D=\Delta ={{b}^{2}}-4ac$ in our equation, we get, ${{b}^{2}}-4ac=0.$
$\Rightarrow {{\left( 2\left( k+2 \right) \right)}^{2}}-4\times \left( 4-k \right)\left( 8k+1 \right)=0$
Opening the square using the formula ${{\left( x+y \right)}^{2}}={{x}^{2}}+{{y}^{2}}+2xy,$ we get,
$\Rightarrow {{2}^{2}}\left( {{k}^{2}}+4+4k \right)-4\left( 4-k \right)\left( 8k+1 \right)=0$
Solving further, we have,
$\Rightarrow 4\left[ {{k}^{2}}+4+4k-\left[ 8k\times 4+4-8{{k}^{2}}-k \right] \right]=0$
$\Rightarrow {{k}^{2}}+4+4k-32k-4+8{{k}^{2}}+k=0$
$\Rightarrow 9{{k}^{2}}-27k=0$
Cancelling 9 by taking the common
$\Rightarrow 9\left( {{k}^{2}}-3k \right)=0$
As, $9\ne 0,$
$\Rightarrow {{k}^{2}}-3k=0$
$\Rightarrow k\left( k-3 \right)=0$
$\Rightarrow k=0;k=3$
Therefore, for the term $\left( 4-k \right){{x}^{2}}+2\left( k+2 \right)x+\left( 8k+1 \right)$ to be a perfect square, k = 0 or k = 3.
Hence, option (d) is the right answer.

Note: The case when the roots are equal is represented graphically as

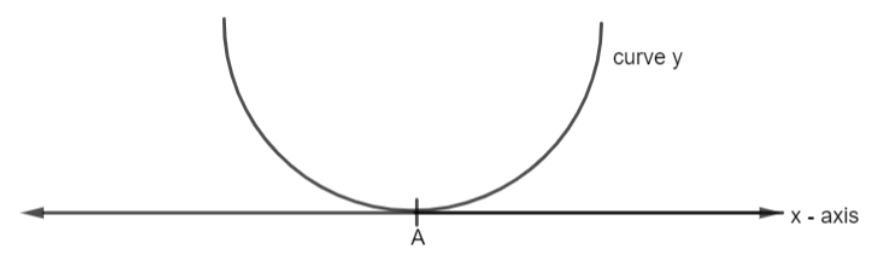
At point A, $D={{b}^{2}}-4ac=0,$ that is discriminant is zero and hence the roots are equal. For single roots, the curve cuts the x-axis once. For example, we have a single root at B.