Question

For what triplets of real numbers (a, b, c) with a ≠ 0 the function:

$f(x) = \begin{cases} x & x \leq 1 \\ ax^2 + bx + c & \text{otherwise} \end{cases}$

is differentiable for all real x ?

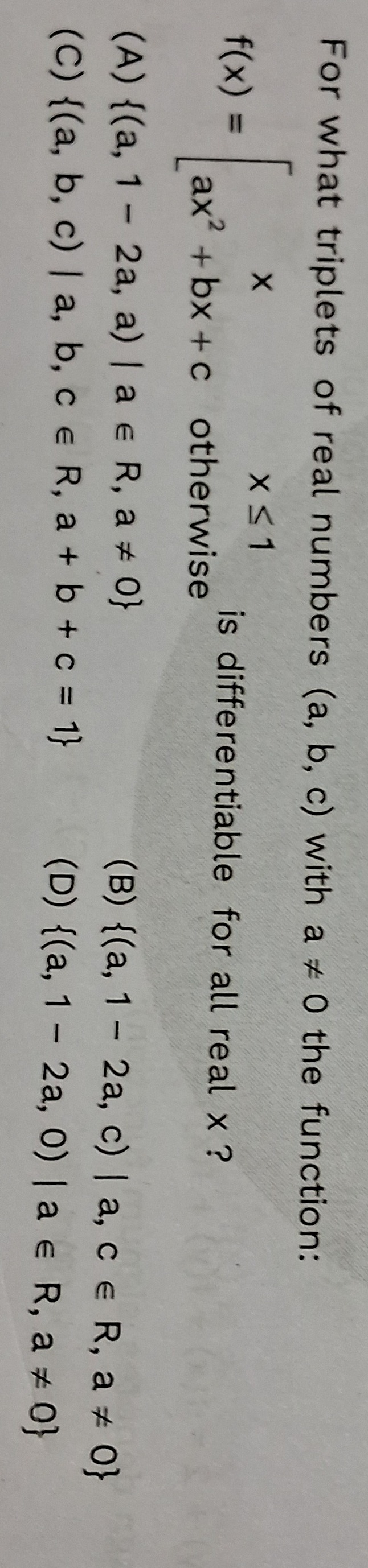
• A. {(a, 1 - 2a, a) | a ∈ R, a ≠ 0}
• B. {(a, 1 – 2a, c) | a, c∈ R, a ≠ 0}
• C. {(a, b, c) | a, b, c ∈ R, a + b + c = 1}
• D. {(a, 1 – 2a, 0) | a ∈ R, a ≠ 0}

Answer 1

Answer: (A)

(A) {(a, 1 - 2a, a) | a ∈ R, a ≠ 0}

Answer 2

For the function $f(x)$ to be differentiable for all real $x$, it must be continuous and differentiable at $x=1$.

1. Continuity at $x=1$: $f(1^-) = f(1^+) = f(1)$. $1 = a(1)^2 + b(1) + c \implies a+b+c=1$.

2. Differentiability at $x=1$: $f'(1^-) = f'(1^+)$. $f'(x) = 1$ for $x<1$, so $f'(1^-)=1$. $f'(x) = 2ax+b$ for $x>1$, so $f'(1^+)=2a+b$. Thus, $2a+b=1$.

Solving the system of equations: $b = 1-2a$ (from $2a+b=1$) Substitute $b$ into $a+b+c=1$: $a + (1-2a) + c = 1 \implies -a+1+c=1 \implies c=a$. Given $a \neq 0$, the triplets are of the form $(a, 1-2a, a)$.