Question

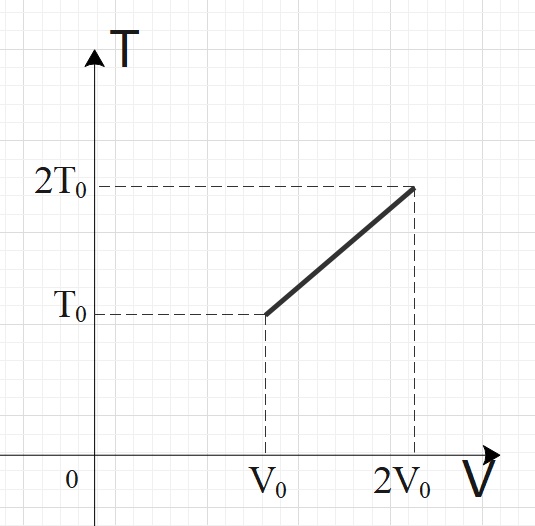
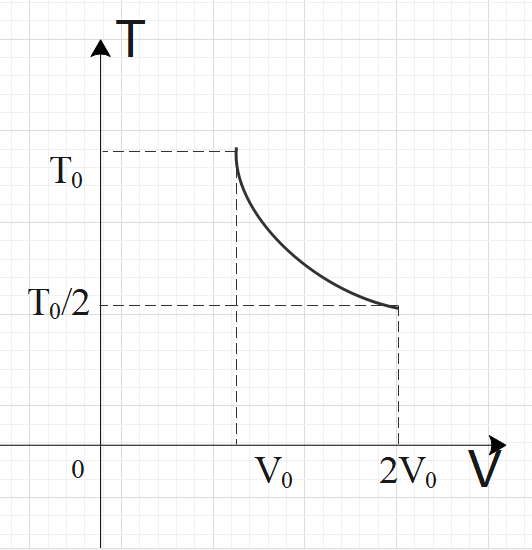
For two thermodynamic processes, temperature and volume diagrams are given. In the first process, it is a straight line having initial and final coordinates as $\left( {{V}_{0}},{{T}_{0}} \right)$and $\left( 2{{V}_{0}},2{{T}_{0}} \right)$, where as in the second process it is a rectangular hyperbola having initial and final coordinates $\left( {{V}_{0}},{{T}_{0}} \right)$ and $\left( 2{{V}_{0}},\dfrac{{{T}_{0}}}{2} \right)$. Then ratio of work done in the two processes must be

a) $1:2$
b) $2:1$
c) $1:1$
d) None of the above

Answer 1

For an ideal gas, $PV=nRT$ is applicable. In graph-1, we have a straight-line relation between temperature and volume, so we can say by ideal gas relation that pressure is constant in graph-1. For the second graph, we have a rectangular hyperbola relation between temperature and volume, i.e. $TV=C$. From both the relations, get the pressure in terms of temperature and volume. Now, calculate the work done by using the formula: $W=\int\limits_{{{V}_{1}}}^{{{V}_{2}}}{PdV}$ and compare the work done by both the processes to get the required ratio.

Complete step by step answer:

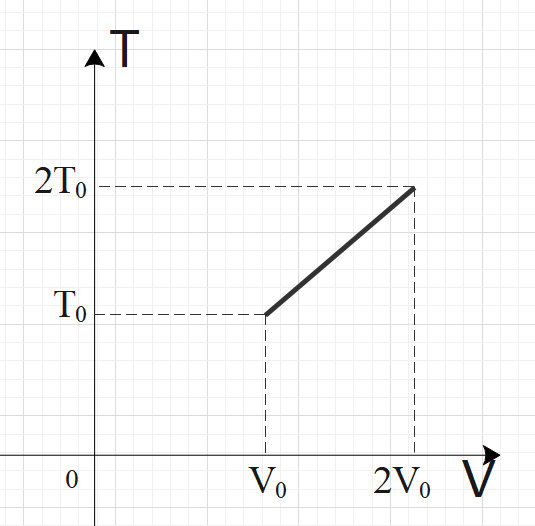
In the first process, we have a straight-line graph, i.e. the slope of the T-V graph is constant.
So, we can say that: $\dfrac{T}{V}=C$
By ideal gas relation, we have: $PV=nRT$
We can also write the ideal gas equation as:
$\dfrac{P}{nR}=\dfrac{T}{V}$
Since $\dfrac{T}{V}=C$, we can say that P is constant.
Now, we need to find the work done by the process 1
As we know that, $W=\int\limits_{{{V}_{1}}}^{{{V}_{2}}}{PdV}$
So, for process-1, we can say: ${{W}_{1}}=\int\limits_{{{V}_{0}}}^{2{{V}_{0}}}{PdV}$
By ideal gas equation, $PV=nRT$
We have:
$PdV=nRdT$
So, we can write work done as:

& {{W}_{1}}=\int\limits_{{{T}_{0}}}^{2{{T}_{0}}}{nRdT} \\\ & =nR\left( T \right)_{{{T}_{0}}}^{2{{T}_{0}}} \\\ & =nR\left( 2{{T}_{0}}-{{T}_{0}} \right) \\\ & =nR{{T}_{0}} \end{aligned}$$  In process-2, we have a rectangular parabola, so we have:$TV=C$ From this result, we can say that: $T=\dfrac{C}{V}$ Now, we know that: $W=\int\limits_{{{V}_{1}}}^{{{V}_{2}}}{PdV}$ So, for process-2, we can say: ${{W}_{2}}=\int\limits_{{{V}_{0}}}^{2{{V}_{0}}}{PdV}$ By ideal gas equation, $PV=nRT$ We have: $P=\dfrac{nRT}{V}$ So, we can write work done as: $$\begin{aligned} & {{W}_{2}}=\int\limits_{{{V}_{0}}}^{2{{V}_{0}}}{PdV} \\\ & =\int\limits_{{{V}_{0}}}^{2{{V}_{0}}}{\dfrac{nRT}{V}dV} \\\ & =nRC\int\limits_{2{{V}_{0}}}^{2{{V}_{0}}}{\dfrac{1}{{{V}^{2}}}dV} \\\ & =nRC\left( -\dfrac{1}{V} \right)_{2{{V}_{0}}}^{2{{V}_{0}}} \end{aligned}$$ So, from graph, we can write: $$\begin{aligned} & {{W}_{2}}=nR\left( -T \right)_{{{T}_{0}}}^{{{T}_{0}}/2} \\\ & =nR\left( -\dfrac{{{T}_{0}}}{2}+{{T}_{0}} \right) \\\ & =\dfrac{nR{{T}_{0}}}{2} \end{aligned}$$ Now, comparing work done by both the processes, we have: $\begin{aligned} & \dfrac{{{W}_{1}}}{{{W}_{2}}}=\dfrac{nR{{T}_{0}}}{\dfrac{nR{{T}_{0}}}{2}} \\\ & \dfrac{{{W}_{1}}}{{{W}_{2}}}=\dfrac{2}{1} \end{aligned}$ So, the required ratio is $1:2$ **So, the correct answer is “Option A”.** **Note:** There is an alternate method to solve the graphs. As we know that work done by a function is the area under the PV curve. So, we can convert these graphs into P-V graphs and then find the area under the curve to get work done.