Question

For two matrices $A = \begin{bmatrix} 3 & -6 & -1 \\ 2 & -5 & -1 \\ -2 & 4 & 1 \end{bmatrix}$ and $B = \begin{bmatrix} 1 & -2 & -1 \\ 0 & -1 & -1 \\ 2 & 0 & 3 \end{bmatrix}$, find the product $AB$ and hence solve the system of equations:

$3x - 6y - z = 3$ $2x - 5y - z + 2 = 0$ $-2x + 4y + z = 5$

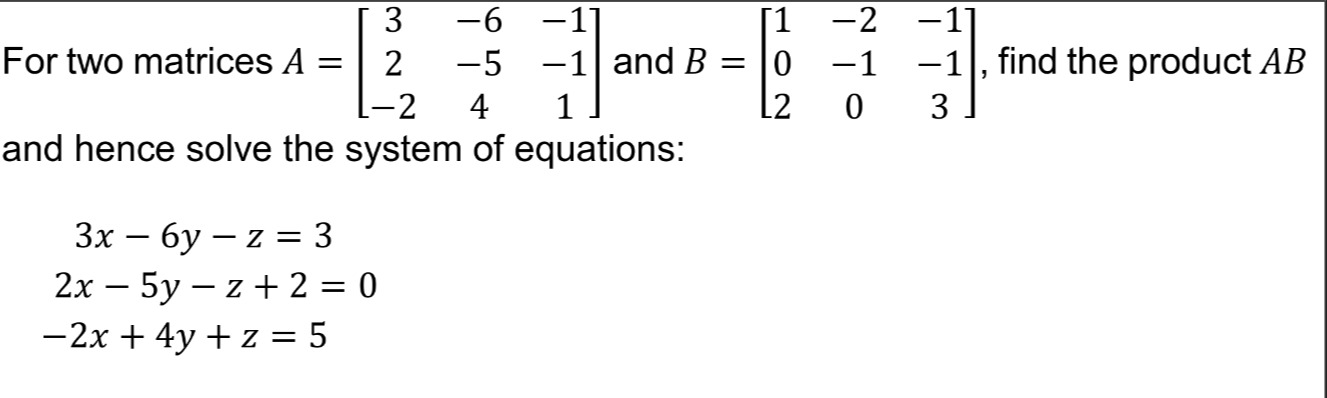
Answer 1

The product $AB$ is the identity matrix $I = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$, and the solution to the system of equations is $x=2$, $y=-3$, $z=21$.

Answer 2

First, calculate the product $AB$. If $AB=I$, then $B$ is the inverse of $A$ ($A^{-1}=B$). The system of equations can be written as $AX=C$. The solution is $X=A^{-1}C$. Substituting $A^{-1}=B$, we get $X=BC$. Calculate $BC$ to find the values of $x, y, z$. $AB = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$ $AX = \begin{bmatrix} 3 & -6 & -1 \\ 2 & -5 & -1 \\ -2 & 4 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 3 \\ -2 \\ 5 \end{bmatrix}$ $X = BC = \begin{bmatrix} 1 & -2 & -1 \\ 0 & -1 & -1 \\ 2 & 0 & 3 \end{bmatrix} \begin{bmatrix} 3 \\ -2 \\ 5 \end{bmatrix} = \begin{bmatrix} 2 \\ -3 \\ 21 \end{bmatrix}$