Question

For three events A, B and C, P(exactly one of the events A or B) $=$ P(exactly one of the events B or C) $=$ P(exactly one of the events C or A) $=$ P and P(all the three events occur simultaneously) $={{P}^{2}}$ , where 0$<$P$<$ $\dfrac{1}{2}$ . If the probability of at least one of the three events A, B and C occurs is $\dfrac{11}{18}$ , the value of P is
(a) $\dfrac{1}{6}$
(b) $\dfrac{1}{4}$
(c) $\dfrac{1}{5}$
(d) $\dfrac{1}{3}$

Answer 1

Hint: First, we should know that $P\left( A\text{ or }B \right)$ means either $P\left( A \right)$ will occur or $P\left( B \right)$ will occur and subtracting the intersection part from set. Similarly, $P\left( \text{B or C} \right)$ and $P\left( \text{C or A} \right)$ writing the 3 equation for this using the formula $P\left( A\cup B \right)=P\left( A \right)+P\left( B \right)-P\left( A\cap B \right)$ . Then adding all the 3 equations so, answer will be in terms of P. Then probability of all three events is given, so adding the value of event with the value of above 3 equation and thus finding the answer of P.

Complete step-by-step answer:
Now, we are given with, P (exactly one of the events A or B) having value equal to P which is written as
$P\left( A\text{ or }B \right)=P\left( A \right)+P\left( B \right)-2P\left( A\cap B \right)=P$ ……………………………(i)
The above equation can be explained by showing Venn diagram i.e.

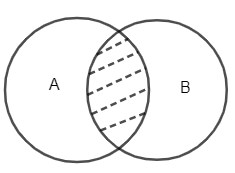
Here, shaded part is called intersection i.e. $P\left( A\cap B \right)$
Now, it is told that either event A will occur or event B so, if A is occurring than intersection part should be subtracted and is B event is occurring than also intersection part should be subtracted because it contains elements of set A as well as B. Therefore, we have subtracted 2 times intersection part in equation (i).
Similarly, we will write remaining two equation i.e. P (exactly one of the events B or C)
$P\left( \text{B or C} \right)=P\left( B \right)+P\left( C \right)-2P\left( B\cap C \right)=P$ ……………….………….(ii)
For P (exactly one of the events C or A)
$P\left( \text{C or A} \right)=P\left( C \right)+P\left( A \right)-2P\left( C\cap A \right)=P$ …………………………………(iii)
Now adding above 3 equation, we get as
$\Rightarrow 2P\left( A \right)+2P\left( B \right)+2P\left( C \right)-2P\left( A\cap B \right)-2P\left( B\cap C \right)-2P\left( C\cap A \right)=3P$ ……………………(iv)
Also, another data is given that P (all the three events occur simultaneously) $={{P}^{2}}$ . So, in mathematical form it is written as
$P\left( A\cup B\cup C \right)={{P}^{2}}$ …………………………(v)
If at least any one event occurs then its probability is given as $P\left( A\text{ or }B\text{ or }C \right)=\dfrac{11}{18}$ …………..(vi)
Now, solving equation (iv) we get
$\Rightarrow P\left( A \right)+P\left( B \right)+P\left( C \right)-P\left( A\cap B \right)-P\left( B\cap C \right)-P\left( C\cap A \right)=\dfrac{3P}{2}$
Now, we know that formula for finding at least one event occur is given as
$\Rightarrow P\left( A\text{ or }B\text{ or }C \right)=P\left( A\cup B\cup C \right)+P\left( A \right)+P\left( B \right)+P\left( C \right)-P\left( A\cap B \right)-P\left( B\cap C \right)-P\left( C\cap A \right)$
We have all the values with us so, just substituting it in above equation, we get
$\Rightarrow \dfrac{11}{18}={{P}^{2}}+\dfrac{3P}{2}$
On solving further, we get
$\Rightarrow \dfrac{11\times 2}{18}=2{{P}^{2}}+3P$
$\Rightarrow \dfrac{11}{9}=2{{P}^{2}}+3P$ ………………………………….(vii)
Now, we can just directly solve using option value and comparing LHS and RHS.
So, taking $\dfrac{1}{3}$ as it is given that the range of P is from 0 to 0.5. So, on putting $\dfrac{1}{3}$ in equation (vii) on RHS side, we get
$=2{{\left( \dfrac{1}{3} \right)}^{2}}+3\left( \dfrac{1}{3} \right)$
$=\dfrac{2}{9}+1$
$=\dfrac{2+9}{9}=\dfrac{11}{9}$
Thus, our LHS is also $\dfrac{11}{9}$ . So, the value of P is $\dfrac{11}{9}$ .
Hence, option (d) is the correct answer.

Note: Be careful with the formula of union as the general formula of A union B is given as $P\left( A\cup B \right)=P\left( A \right)+P\left( B \right)-P\left( A\cap B \right)$ but we are given A “OR'' B in the question so 2 times intersection will be subtracted. If you miss this subtraction then the whole answer will go wrong. Also, in finding value of P from quadratic equation form, it will take some time to solve in finding factors and will become complex. So, it's better sometimes to go with the option method and find an answer easily.