Question

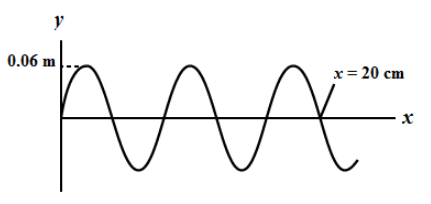
For the wave shown in the figure, find its amplitude, frequency and wavelength if its speed is 300 m/s. Write the equation of this wave as it travels out along the +x-axis if its position at $t = 0$ is as shown.

Answer 1

We know that the amplitude of the wave is the oscillations from the mean position. The total horizontal distance has five half wavelengths. Use this concept to determine the wavelength. We can use the relation between velocity, wavelength and frequency to determine the frequency of the wave. Use the relation between angular frequency and frequency to determine the angular frequency.

Formula used:
$v = f\lambda$
Here, v is the velocity of the particle, f is the frequency and $\lambda$ is the wavelength.
$f = \dfrac{v}{\lambda }$
$\omega = 2\pi f$
$v = \dfrac{\omega }{k}$
Here, $\omega$ is the angular frequency and k is the wave-number.

Complete step by step answer:
We know that the amplitude of the wave is the oscillations from the mean position. In the given figure, the maximum distance from the mean position is 0.06 m. Therefore, we can say that the amplitude of the wave is 0.06 m.
$A = 0.06\,m$
In the given figure, we observe there are five half wavelengths in 20 cm distance. Therefore, we can express this distance as,
$20\,cm = 5\left( {\dfrac{\lambda }{2}} \right)$
$\Rightarrow \lambda = \dfrac{{40}}{5}$
$\Rightarrow \lambda = 8\,cm$
Therefore, the wavelength of the wave is 8 cm or 0.08 m.
We have the relation between velocity, wavelength and frequency as,
$v = f\lambda$
Here, v is the velocity of the particle, f is the frequency and $\lambda$ is the wavelength.
We rearrange the above equation for f as follows,
$f = \dfrac{v}{\lambda }$
We substitute 300 m/s for v and 8 cm for $\lambda$ in the above equation.
$f = \dfrac{{300\,m/s}}{{0.08\,m}}$
$\Rightarrow f = 3750\,Hz$
Thus, the frequency of the wave is 3750 Hz.
We know the displacement equation of the particle is given as,
$x = A\sin \left( {kx - \omega t} \right)$ …… (1)
We have to determine the angular frequency and wave-number k of the given wave.
We know the relation,
$\omega = 2\pi f$
We substitute 3750 Hz for f in the above equation.
$\omega = 2\pi \left( {3750} \right)$
$\Rightarrow \omega = 7500\pi \,rad/s$
We also know the relation,
$v = \dfrac{\omega }{k}$
$\Rightarrow k = \dfrac{\omega }{v}$
We substitute $\omega = 7500\pi \,rad/s$ and $v = 300\,m/s$ in the above equation.
$k = \dfrac{{7500\pi }}{{300}}$
$\therefore k = 25\pi$

Therefore, we can write the wave equation (1) as,$x = 0.06\sin \left( {25\pi x - 7500\pi t} \right)$.

Note: To solve this type of question from the given wave, students should be able to calculate the wavelength of the wave. Note that amplitude is not distance between the extreme positions of the particle performing oscillations. It is the distance from the mean positions to the extreme position. The unit of frequency is hertz or per second while the unit of angular frequency is rad/sec.