Solveeit Logo
Login

Question

Question: For the vector in fig., with \(a = 4\), \(b = 3\) and \(c = 5\), what are (a) the magnitude and (b) ...

For the vector in fig., with a=4a = 4, b=3b = 3 and c=5c = 5, what are (a) the magnitude and (b) the direction of a⃗×c⃗\vec{a} \times \vec{c} (c) the magnitude and (d) the direction of a⃗×b⃗\vec{a} \times \vec{b}, and the magnitude and (f) the direction of b⃗×c⃗\vec{b} \times \vec{c}(the z-axis is not shown)

Explanation

Solution

Cross product is a binary procedure on two vectors in 3−D3-D space. Given two linearly independent vectors, a and b, the cross product of a and b is a perpendicular vector to both a and b. If two vectors have the identical direction or have the opposite direction from one another or have zero length, then their vector product is zero.

Complete step-by-step solution:
Given: ∣a⃗∣=4|\vec{a}| = 4, ∣b⃗∣=3|\vec{b}| = 3, ∣c⃗∣=5|\vec{c}| = 5

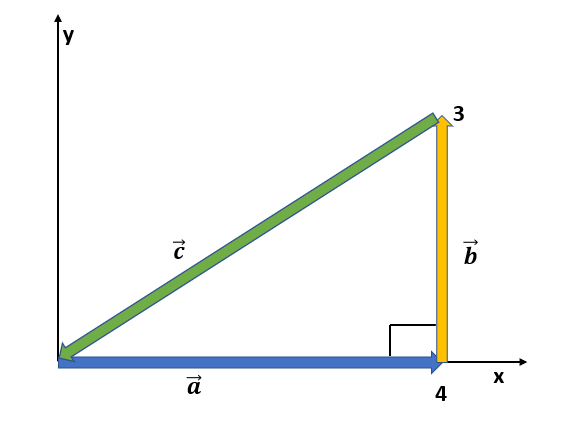
From figure, a⃗=4i^\vec{a} = 4 \hat{i}, b⃗=3j^\vec{b} = 3 \hat{j} and c⃗=4i^+3j^\vec{c} = 4 \hat{i} + 3 \hat{j}
a) First, we find the magnitude of a⃗×c⃗\vec{a} \times \vec{c},
a⃗×c⃗=4i^×(4i^+3j^)\vec{a} \times \vec{c} = 4 \hat{i} \times (4 \hat{i} + 3 \hat{j})
a⃗×c⃗=16(i^×i^)+12(i^×j^)\vec{a} \times \vec{c} = 16 (\hat{i} \times \hat{i}) + 12 (\hat{i} \times \hat{j})
a⃗×c⃗=12k^\vec{a} \times \vec{c} = 12 \hat{k}
b) The direction of a⃗×c⃗\vec{a} \times \vec{c} is k^\hat{k}.
c) Now, we find the magnitude a⃗×b⃗\vec{a} \times \vec{b},
a⃗×b⃗=4i^×3j^\vec{a} \times \vec{b} = 4 \hat{i} \times 3 \hat{j}
a⃗×b⃗=12(i^×j^)\vec{a} \times \vec{b} = 12 (\hat{i} \times \hat{j})
a⃗×b⃗=12k^\vec{a} \times \vec{b} = 12 \hat{k}
d) The direction of a⃗×b⃗\vec{a} \times \vec{b} is k^\hat{k}.
e) First, we find the magnitude of b⃗×c⃗\vec{b} \times \vec{c}
b⃗×c⃗=3j^×(4i^+3j^)\vec{b} \times \vec{c} = 3 \hat{j} \times (4 \hat{i} + 3 \hat{j})
b⃗×c⃗=12(j^×i^)+9(j^×j^)\vec{b} \times \vec{c} = 12 (\hat{j} \times \hat{i}) + 9 (\hat{j} \times \hat{j})
b⃗×c⃗=−12k^\vec{b} \times \vec{c} = -12 \hat{k}
f) The direction of b⃗×c⃗\vec{b} \times \vec{c} is −k^\hat{-k}.

Note: More commonly, the magnitude of the cross product is equal to the area of a parallelogram with vectors for sides; in particular, the magnitude of the product of two perpendicular vectors is the product of their lengths. The right-hand thumb rule is utilized in which we turn up the fingers of the right hand about a line perpendicular to the vectors planes a and b and fold the fingers in the way from a to b, then the extended thumb points in the way of c.