Question

For the three dumbbells shown above, the rod connecting them has a negligible mass and has a length of $d$. The spheres shown in Dumbbell 1 and Dumbbell 2 have a uniform density of $\rho$and the spheres in Dumbbell 3 has a density of $2\rho$. For which dumbbell is the centre of mass furthest to the left?

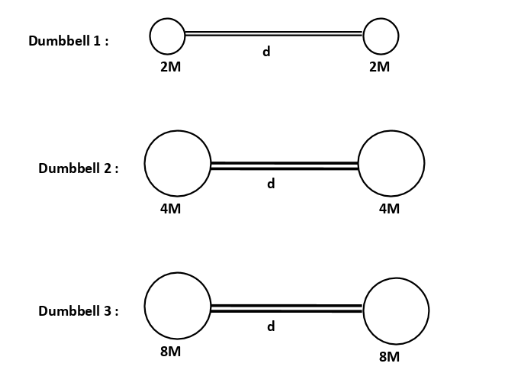
A. Dumbbell 1
B. Dumbbell 2
C. Dumbbell 3
D. The location of the centre of mass is the same for all the three dumbbells.

Answer 1

The centre of mass of a rigid body is a fixed point. But, the centre of mass of two particles lies in between the line joining the two particles. Here, the masses on both sides of each dumbbell are the same. Therefore, the centre of mass should lie between the rod that joins the two ends.

Formula Used:
The centre of mass for two objects is given by the formula:
${R_{cm}} = \dfrac{{{m_1}{r_1} + {m_2}{r_2}}}{{{m_1} + {m_2}}}$ $\to (1)$
Where, ${R_{cm}}$is the centre of mass, ${m_1}$ is the mass of first object and ${m_2}$ is the mass of the second object, ${r_1}$ is the distance of the first object from the origin and ${r_2}$ is the distance of the second object from the origin.

Complete step by step answer:
In the given problem, the two masses are equal. That is, ${m_1} = {m_2}$. Then from equation (1);

\Rightarrow {R_{cm}} = \dfrac{{{m_1}\left( {{r_1} + {r_2}} \right)}}{{2{m_1}}} \\\ \Rightarrow {R_{cm}} = \dfrac{{{r_1} + {r_2}}}{2}$$ $$ \to (2)$$ Consider Dumbbell 1. Then, $${m_1} = 2M$$. Let the mass $$2M$$ be at the origin. Therefore, $${r_1} = 0$$. The second mass is $${m_2} = 2M$$ and is located at a distance $$d$$ from the origin. Therefore, $${r_2} = d$$. Thus, from equation (2), $${R_{cm}} = \dfrac{{0 + d}}{2} \therefore {R_{cm}} = \dfrac{d}{2}$$. Similar calculations can be made for Dumbbell 2 and Dumbbell 3. Thus for all the dumbbells, the centre of mass lies at the centre of the rod the two masses. Therefore, The location of the centre of mass is the same for all the three dumbbells since the connecting rod has length $$d$$ for all the dumbbells. **Hence, option D is the correct answer.** **Note:** It is mentioned in the problem that the spheres in Dumbbell 1 and Dumbbell 2 have a uniform density of $$\rho $$ and the spheres in Dumbbell 3 have a density of $$2\rho $$. These opposite spheres of each dumbbell also have equal masses. This means that they have equal volumes too. The location of the centre of the mass of the body does not depend on the choice of the coordinate system. Even if the first mass is taken at the origin and the second mass is taken at a distance $$d$$ from the origin, then also the centre of the mass for the dumbbell remains at the same location.