Question
Question: For the system shown which of the option(s) are CORRECT : ...
For the system shown which of the option(s) are CORRECT :
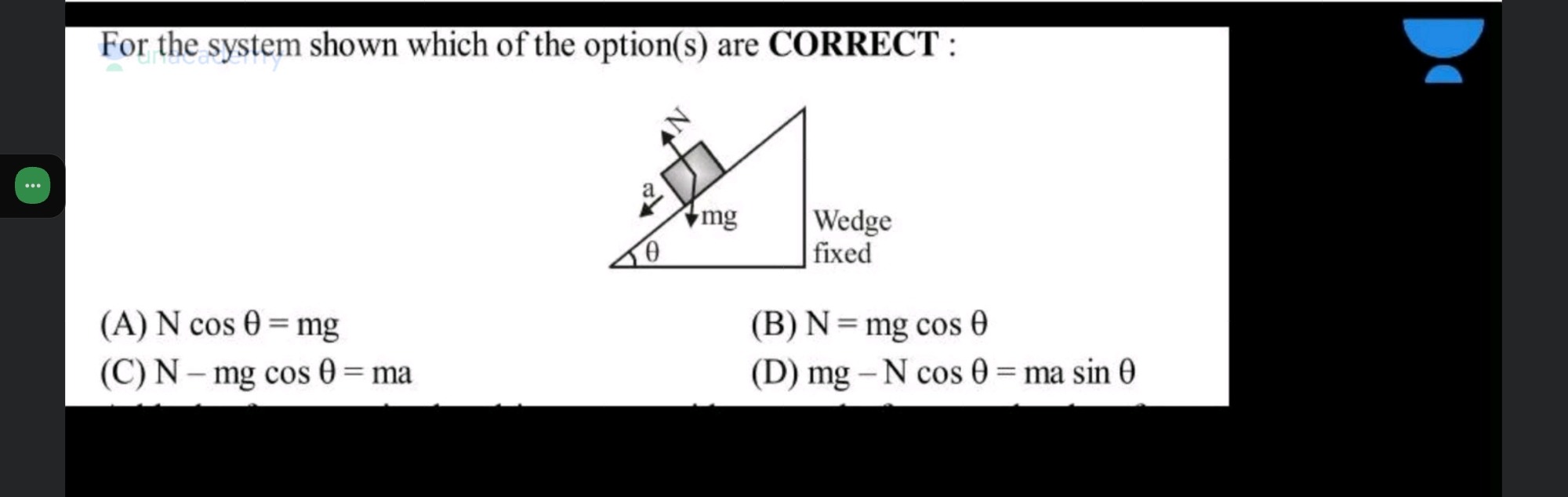
N cos θ = mg
N = mg cos θ
N – mg cos θ = ma
mg – N cos θ = ma sin θ
B, D
Solution
To solve this problem, we need to analyze the forces acting on the block and apply Newton's Second Law of Motion. We will use two different coordinate systems to check all the given options.
1. Free Body Diagram and Force Resolution:
Let's draw the free body diagram for the block.
- Weight (mg): Acts vertically downwards.
- Normal Force (N): Acts perpendicular to the inclined surface, upwards.
- Acceleration (a): The block accelerates down the incline.
We can resolve the forces into components along two different sets of axes:
Method 1: Axes parallel and perpendicular to the inclined plane.
-
Perpendicular to the incline (y-axis):
The block is not accelerating perpendicular to the incline. Therefore, the net force in this direction is zero.
The component of gravity perpendicular to the incline is
mg cos θ(acting downwards into the incline).The normal force N acts upwards, away from the incline.
Applying Newton's Second Law (ΣF_y = ma_y):
N−mgcosθ=0
N=mgcosθ
This equation matches Option (B). So, (B) is correct.
-
Parallel to the incline (x-axis):
The block is accelerating down the incline with acceleration 'a'.
The component of gravity parallel to the incline is
mg sin θ(acting downwards along the incline).Assuming no friction or friction is overcome, this is the net force causing acceleration.
Applying Newton's Second Law (ΣF_x = ma_x):
mgsinθ=ma
Method 2: Horizontal and Vertical axes.
-
Forces:
-
Weight (mg): Acts only in the vertical direction (downwards).
-
Normal Force (N): This force is perpendicular to the inclined plane. The angle of the incline is θ. This means the normal force N makes an angle θ with the vertical axis.
- Horizontal component of N: Nx=Nsinθ (acting to the left)
- Vertical component of N: Ny=Ncosθ (acting upwards)
-
-
Acceleration (a): The acceleration 'a' is directed down the incline. We need to find its horizontal and vertical components.
- Horizontal component of 'a': ax=acosθ (acting to the right)
- Vertical component of 'a': ay=asinθ (acting downwards)
-
Applying Newton's Second Law:
-
Vertical Direction (downwards positive):
Sum of vertical forces = mass × vertical acceleration
mg−Ncosθ=m(asinθ)
mg−Ncosθ=masinθ
This equation matches Option (D). So, (D) is correct.
-
Horizontal Direction (right positive):
Sum of horizontal forces = mass × horizontal acceleration
−Nsinθ=m(−acosθ)
Nsinθ=macosθ
-
Checking other options:
- (A) N cos θ = mg: This is incorrect. From Method 1, we found N = mg cos θ, which means N/cos θ = mg.
- (C) N – mg cos θ = ma: This is incorrect. From Method 1, N - mg cos θ = 0, as there is no acceleration perpendicular to the incline.
Therefore, both options (B) and (D) are correct.
Explanation of the solution:
- Coordinate System 1 (Perpendicular to Incline): Resolve forces perpendicular to the inclined plane. The net force perpendicular to the incline is zero because the block does not accelerate in that direction. The normal force (N) acts perpendicular to the surface, and the component of gravity perpendicular to the surface is
mg cos θ. Equating these givesN - mg cos θ = 0, leading toN = mg cos θ. This confirms option (B). - Coordinate System 2 (Vertical): Resolve forces in the vertical direction. The gravitational force
mgacts vertically downwards. The normal forceNhas a vertical componentN cos θacting upwards. The accelerationaalong the incline has a vertical componenta sin θacting downwards. Applying Newton's second law vertically (ΣF_y = ma_y), we getmg - N cos θ = ma sin θ. This confirms option (D).
