Question
Question: For the system shown in the figure the pulleys are light and frictionless the tension in the string ...
For the system shown in the figure the pulleys are light and frictionless the tension in the string will be?
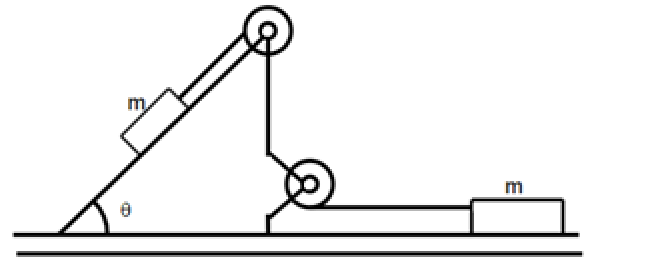
A). (32)mgsinθ
B). 21mgsinθ
C). (23)mgsinθ
D). 2mgsinθ
Solution
Tension is the pulling force transmitted axially by the means of a string. A string which has only one dimension that is length the tension in a string is a non negative scalar quantity and the tension along the string is obtained by Newton's third law of motion and it states that for every action there will be equal and opposite reaction.
Complete step-by-step solution:
Consider a block of mass (m) which is suspended to a string .The string which has negligible mass. The string is being stretched and pulled by oppositely directed forces of the same magnitude and by newton’s third law the string exerts oppositely directed forces of equal magnitude. These forces act to oppose the stretching of the string. If the acceleration is zero the block is assumed to be in equilibrium then the tension in the string is given by
T−mg=0
Tension for block on the horizontal plane,
From the fig, 1. We can find that the force acting on the block is just the tension which is in the same direction of the net force. The net force is given as below
T=ma ⋯⋯(1)
Tension for block on the inclined plane,
From the fig, 1.We can find that the tension force and the applied force are acting in different directions. So the net force is given as below
ma=mgsinθ−T
Substituting equation (1)
T=mgsinθ−T ⋯⋯(2)
On rearranging
T=(21)mgsinθ
So the correct option is C.
Note: Student’s tension on string is different for different blocks which are inclined at different angles. Rope can be used to pull heavy objects. When we pull a rope there will be tension and in this problem we are neglecting the frictional force and the tension on the string is obtained by Newton's law of motion.
