Question

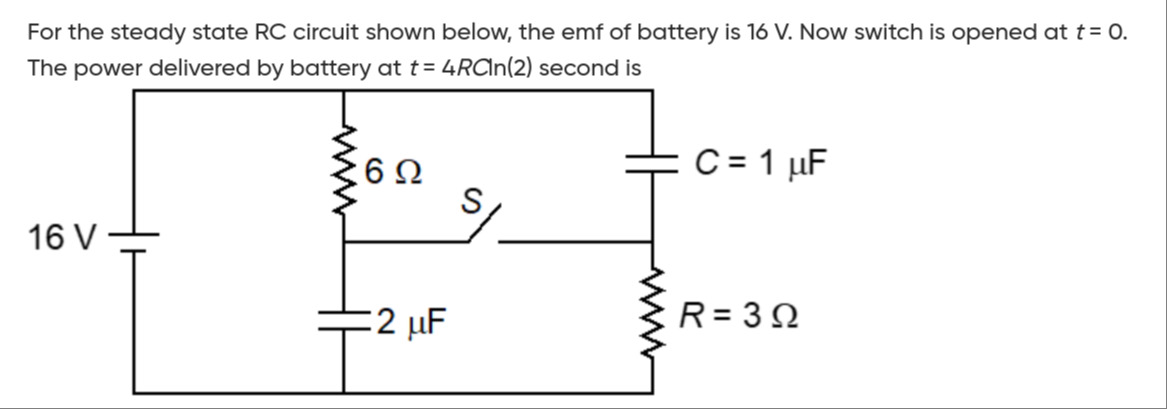
For the steady state RC circuit shown below, the emf of battery is 16 V. Now switch is opened at t = 0. The power delivered by battery at t = 4RCIn(2) second is

Answer 1

16 W

Answer 2

The problem asks for the power delivered by the battery at a specific time $t = 4RC\ln(2)$ after the switch is opened. We need to analyze the circuit in three stages:

1. Steady state before the switch is opened ($t < 0$).
2. Immediately after the switch is opened ($t = 0+$).
3. For $t > 0$, to find the current through the battery.

1. Steady state (t < 0) - Switch S is closed

In steady state, capacitors act as open circuits for DC current.

Let's label the nodes:

• Top wire: 16 V
• Bottom wire: 0 V (ground)
• Node A: Between the 6 $\Omega$ resistor, $C_1$ (2 $\mu F$), and switch S.
• Node B: Between switch S, $C_2$ (1 $\mu F$), and $R$ (3 $\Omega$).

Since $C_1$ and $C_2$ are open circuits, no current flows through them.

The circuit effectively becomes: 16 V battery $\rightarrow$ 6 $\Omega$ resistor $\rightarrow$ Switch S (closed) $\rightarrow$ 3 $\Omega$ resistor $\rightarrow$ 0 V.

The 6 $\Omega$ and 3 $\Omega$ resistors are in series.

Total resistance $R_{eq} = 6 \Omega + 3 \Omega = 9 \Omega$.

The current flowing from the battery in steady state ($I_0$) is:

$I_0 = \frac{16 \text{ V}}{9 \text{ }\Omega} = \frac{16}{9} \text{ A}$.

Now, let's find the initial voltages across the capacitors:

Voltage across the 6 $\Omega$ resistor: $V_{6\Omega} = I_0 \times 6 \Omega = \frac{16}{9} \times 6 = \frac{32}{3} \text{ V}$.

Potential at Node A: $V_A = 16 \text{ V} - V_{6\Omega} = 16 - \frac{32}{3} = \frac{48-32}{3} = \frac{16}{3} \text{ V}$.

Since the switch S is closed, $V_B = V_A = \frac{16}{3} \text{ V}$.

Initial voltage across $C_1$: $V_{C1,i} = V_A - 0 \text{ V} = \frac{16}{3} \text{ V}$.

Initial voltage across $C_2$: $V_{C2,i} = 16 \text{ V} - V_B = 16 - \frac{16}{3} = \frac{32}{3} \text{ V}$.

2. At t = 0 (Switch S is opened)

When the switch S is opened, Node A and Node B are disconnected. The circuit effectively splits into two independent RC circuits connected to the battery.

Left RC branch (Battery, 6 $\Omega$, $C_1$):

This branch consists of the 16 V battery, the 6 $\Omega$ resistor, and the $C_1 = 2 \mu F$ capacitor.

The voltage across $C_1$ will charge towards 16 V.

The time constant for this branch is $\tau_1 = R_{6\Omega} C_1 = 6 \Omega \times 2 \mu F = 12 \mu s$.

The voltage across $C_1$ as a function of time is:

$V_{C1}(t) = V_f + (V_{C1,i} - V_f) e^{-t/\tau_1}$

$V_{C1}(t) = 16 + (\frac{16}{3} - 16) e^{-t/12\mu s} = 16 - \frac{32}{3} e^{-t/12\mu s}$.

The current through the 6 $\Omega$ resistor ($I_1(t)$) is the charging current of $C_1$:

$I_1(t) = C_1 \frac{dV_{C1}}{dt} = C_1 \left(0 - \frac{32}{3} \left(-\frac{1}{\tau_1}\right) e^{-t/\tau_1}\right) = \frac{C_1}{\tau_1} \frac{32}{3} e^{-t/\tau_1}$

$I_1(t) = \frac{C_1}{R_{6\Omega} C_1} \frac{32}{3} e^{-t/\tau_1} = \frac{1}{6} \frac{32}{3} e^{-t/12\mu s} = \frac{16}{9} e^{-t/12\mu s}$.

This current $I_1(t)$ flows from the battery.

Right RC branch (Battery, $C_2$, 3 $\Omega$):

This branch consists of the 16 V battery, the $C_2 = 1 \mu F$ capacitor, and the $R = 3 \Omega$ resistor.

The voltage across $C_2$ will discharge (or charge towards 16V, but it's already connected to 16V on one side).

Let's consider the loop: 16V $\rightarrow$ $C_2 \rightarrow R \rightarrow$ 0V.

The initial voltage across $C_2$ is $V_{C2,i} = \frac{32}{3} \text{ V}$.

The positive plate of $C_2$ is connected to 16 V, and the negative plate is at $V_B$.

When S is opened, $C_2$ and $R$ form a series circuit with the battery.

The voltage across $C_2$ is $V_{C2}(t)$. The voltage across $R$ is $V_R(t)$.

Applying KVL: $16 - V_{C2}(t) - V_R(t) = 0$.

The current $I_2(t)$ flows from the battery through $C_2$ and $R$.

$I_2(t) = \frac{V_R(t)}{R} = \frac{16 - V_{C2}(t)}{R}$.

Also, $I_2(t) = C_2 \frac{dV_{C2}}{dt}$.

So, $C_2 \frac{dV_{C2}}{dt} = \frac{16 - V_{C2}(t)}{R}$.

$\frac{dV_{C2}}{dt} = \frac{16 - V_{C2}(t)}{RC_2}$.

This is a charging circuit for $C_2$. The capacitor $C_2$ will charge to 16 V.

The time constant for this branch is $\tau_2 = R C_2 = 3 \Omega \times 1 \mu F = 3 \mu s$.

The voltage across $C_2$ as a function of time is:

$V_{C2}(t) = V_f + (V_{C2,i} - V_f) e^{-t/\tau_2}$

$V_{C2}(t) = 16 + (\frac{32}{3} - 16) e^{-t/3\mu s} = 16 - \frac{16}{3} e^{-t/3\mu s}$.

The current through the 3 $\Omega$ resistor ($I_2(t)$) is:

$I_2(t) = C_2 \frac{dV_{C2}}{dt} = C_2 \left(0 - \frac{16}{3} \left(-\frac{1}{\tau_2}\right) e^{-t/\tau_2}\right) = \frac{C_2}{\tau_2} \frac{16}{3} e^{-t/\tau_2}$

$I_2(t) = \frac{C_2}{R C_2} \frac{16}{3} e^{-t/\tau_2} = \frac{1}{3} \frac{16}{3} e^{-t/3\mu s} = \frac{16}{9} e^{-t/3\mu s}$.

This current $I_2(t)$ also flows from the battery.

3. Total current from the battery for t > 0

The total current delivered by the battery $I_{bat}(t)$ is the sum of currents $I_1(t)$ and $I_2(t)$:

$I_{bat}(t) = I_1(t) + I_2(t) = \frac{16}{9} e^{-t/12\mu s} + \frac{16}{9} e^{-t/3\mu s}$.

$I_{bat}(t) = \frac{16}{9} \left(e^{-t/12\mu s} + e^{-t/3\mu s}\right)$.

We need to find the power delivered by the battery at $t = 4RC\ln(2)$ second.

From the problem statement, $R = 3 \Omega$ and $C = 1 \mu F$. So $RC = 3 \mu s$.

The given time is $t = 4RC\ln(2) = 4(3 \mu s)\ln(2) = 12\ln(2) \mu s$.

Let's substitute $t$ into the expression for $I_{bat}(t)$:

$e^{-t/12\mu s} = e^{-(12\ln(2)\mu s)/12\mu s} = e^{-\ln(2)} = e^{\ln(1/2)} = \frac{1}{2}$.

$e^{-t/3\mu s} = e^{-(12\ln(2)\mu s)/3\mu s} = e^{-4\ln(2)} = e^{\ln(2^{-4})} = 2^{-4} = \frac{1}{16}$.

Now, calculate $I_{bat}(t)$ at this time:

$I_{bat}(t) = \frac{16}{9} \left(\frac{1}{2} + \frac{1}{16}\right) = \frac{16}{9} \left(\frac{8}{16} + \frac{1}{16}\right) = \frac{16}{9} \left(\frac{9}{16}\right) = 1 \text{ A}$.

The power delivered by the battery is $P = V_{battery} \times I_{bat}(t)$.

$P = 16 \text{ V} \times 1 \text{ A} = 16 \text{ W}$.

The final answer is $\boxed{\text{16 W}}$.