Question

For the situations shown in figure, determine the angle by which the mirror should be rotated, so that the light ray will retrace its path after refraction through the prism and reflection from the mirror?
A) 1° ACW
B) 1° CW
C) 2° ACW
D) 2° CW

Answer 1

From the given diagram, we can observe the given quantities. Then draw the ray diagram of light getting refracted (from prism) and reflected (from mirror). It can be analyzed then under what conditions the path of light will be retracted means follow back the same path it came from.

Formula used:
$\delta = \left( {\mu - 1} \right)A$ where $\delta$ is the angle of deviation, $\mu$ is the refractive index and A is the angle of prism
🡪 CW and ACW given in the options denotes clockwise and anticlockwise direction

Complete step by step answer:
The points that can be observed from the given figure are:

Angle of the given prism, A is 4° and its refractive index, $\mu$ is 1.5.
A horizontal ray is striking its surface and we are required to find the angle at which mirror should be rotated so that light follows the same path as it came (retrace the path)
The light striking normal to the surface of the mirror retraces the same path after reflection, so the light ray should make 90° with the mirror. For the light to retrace the same path, the mirror should be rotated at an angle equal to the angle through which light is bent called angle of deviation.

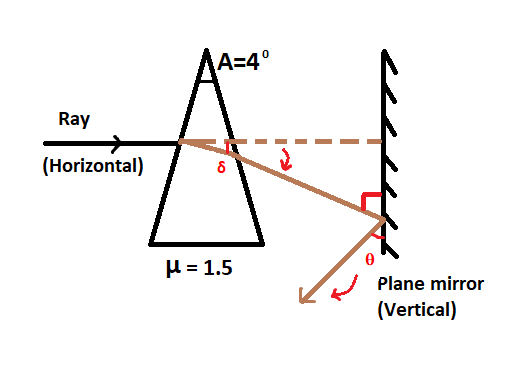
We can calculate the angle of deviation using its relationship with refractive index and angle of prism:
$\delta = \left( {\mu - 1} \right)A$
Substituting the values we get:
$\delta = \left( {1.5 - 1} \right)4 \\\ \Rightarrow\delta = 0.5 \times 4 \\\ \Rightarrow\delta = {2^\circ } \\\$
From the diagram, it can be seen that this rotation of 2° is in clockwise direction.
Angle through which the mirror should rotate is $\theta$ and it should be equal in magnitude and direction of the angle of deviation $\delta$ for the light to retrace its path.
$\Rightarrow \theta = \delta \\\ \Rightarrow \theta = {2^\circ } \\\$
And the direction is clockwise.
Therefore, the mirror should be rotated through an angle of 2° in clockwise direction, so that the light ray will retrace its path after refraction through the prism and reflection from the mirror

So, the correct answer is “Option D”.

Note:
We said the light ray should fall perpendicular to the surface of the mirror for it to retrace the same path, this is because, the law of reflection states that angle of incidence and reflection are equal, so when angle of incidence is 90°, the angle of reflection will also be 90° and the path of light will be retracted.Remember that the refraction takes place when the medium of light changes while travelling and thus will take place in prism while through the mirror, reflection will take place.