Question

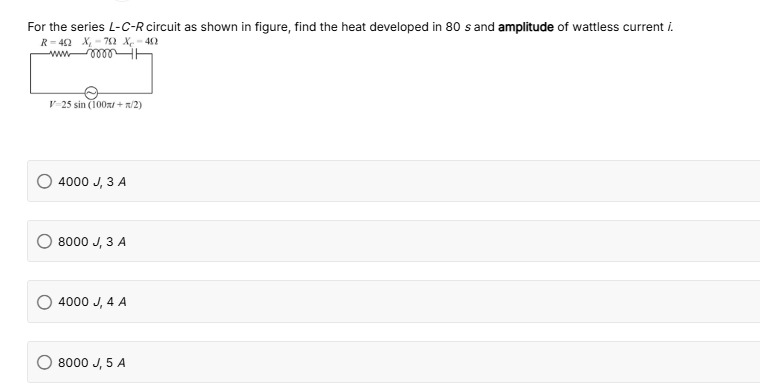
For the series $L-C-R$ circuit as shown in figure, find the heat developed in $80$ $s$ and amplitude of wattless current $i$. $R=4\Omega$ $X_L=7\Omega$ $X_c=4\Omega$ $V = 25 \sin(100\pi t + \pi/2)$

• A. 4000 J, 3 A
• B. 8000 J, 3 A
• C. 4000 J, 4 A
• D. 8000 J, 5 A

Answer 1

Answer: (A)

4000 J, 3 A

Answer 2

1. Calculate the Net Reactance ($X$): $X = X_L - X_C = 7 \Omega - 4 \Omega = 3 \Omega$.

2. Calculate the Impedance ($Z$): $Z = \sqrt{R^2 + X^2} = \sqrt{(4 \Omega)^2 + (3 \Omega)^2} = \sqrt{16 + 9} = \sqrt{25} = 5 \Omega$.

3. Calculate the Amplitude of the Current ($I_0$): From the voltage equation $V = 25 \sin(100\pi t + \pi/2)$, the amplitude of the voltage is $V_0 = 25$ V. $I_0 = \frac{V_0}{Z} = \frac{25 \text{ V}}{5 \Omega} = 5$ A.

4. Calculate the Heat Developed ($H$) in 80 seconds: The RMS current is $I_{rms} = \frac{I_0}{\sqrt{2}} = \frac{5}{\sqrt{2}}$ A. The heat developed is given by $H = I_{rms}^2 R t$. $H = \left(\frac{5}{\sqrt{2}}\right)^2 \times 4 \Omega \times 80 \text{ s} = \frac{25}{2} \times 4 \times 80 = 25 \times 2 \times 80 = 4000$ J.

5. Calculate the Amplitude of the Wattless Current ($I_{wattless}$): The phase angle $\phi$ is given by $\tan \phi = \frac{X}{R} = \frac{3 \Omega}{4 \Omega} = \frac{3}{4}$. From this, we can determine $\sin \phi = \frac{3}{5}$. The amplitude of the wattless current is $I_{wattless} = I_0 \sin \phi$. $I_{wattless} = 5 \text{ A} \times \frac{3}{5} = 3$ A.

Therefore, the heat developed in 80 s is 4000 J, and the amplitude of the wattless current is 3 A.