Question
Question: For the right triangle shown in figure above, what are (a) the length of the unknown side, (b)...
For the right triangle shown in figure above, what are
(a) the length of the unknown side,
(b) the tangent of θ , and
(c) the sine of ϕ ?
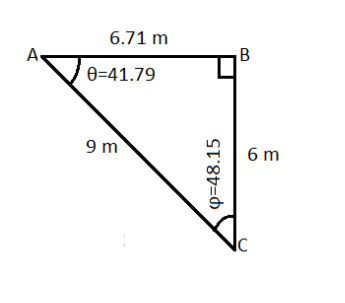
Solution
Hint : Pythagoras theorem: Pythagoras theorem is used in the right angle triangle. It is used to find the one known side if the two sides are given. It states that “the sum of the square of height and base are always equal to the square of hypotenuse. Which triangle fills this criteria is also called a right angle triangle.
As we know that
h2=b2+l2
Here,
h=hypotenuse
b=base
l=height
** Complete step-by-step answer** :
Given,
Length of hypotenuse =9m
Length of height =6m
Using the Pythagoras theorem is given by
⇒h2=b2+l2
So we find the base then,
⇒b=h2−l2
Put the value in equation
⇒b=92−62
⇒b=81−36
⇒b=45
Factorize the 45
⇒45=3×3×5
Put above
⇒b=3×3×5
Make the set and take out from radical
⇒b=35m
⇒b=6.71m
Hence the length of base is 6.71m
(b) Now find the tangent of θ
Tangent is the ratio of side opposite the angle and side adjacent to angle
Side opposite the angle =6m
Side adjacent the angle =6.71m
Put the value
⇒tanθ=6.716
⇒tanθ=0.894
(b) Now find the sine of ϕ
Sine is the ratio of side opposite the angle and hypotenuse of triangle
Side opposite the angle =6.71m
Hypotenuse of the triangle =9m
Put the value
⇒sinϕ=96.71
⇒sinϕ=0.745
Note : Trigonometry is the branch of mathematics which deals with the relationship between side lengths and angle of triangles. There are six trigonometric ratios they are- sine, cosine, tangent, cosecant, secant, and cotangent. And their abbreviations are sin, cos, tan, cot, cosec, and sec. Right Angle Triangle Properties- One angle is always 90° or right angle. The side opposite angle 90° is the hypotenuse. The hypotenuse is always the longest side. The sum of the other two interior angles is equal to 90°. The other two sides adjacent to the right angle are called base and perpendicular.
