Question

For the resistance network shown in the figure, choose the correct option(s).

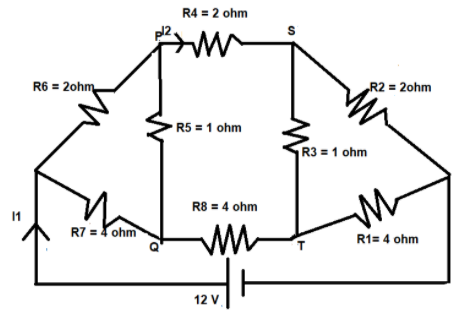
A.The current through PQ is zero.
B.${{I}_{1}}=3A$
C.The potential at S is less than that at Q
D.${{I}_{2}}=2A$

Answer 1

In series-parallel circuits the Wheatstone bridge condition can be applied to simply the problem. Applying the necessary conditions, we can find the equivalent resistance of the circuit and find the current through each resistance and through the entire circuit.

Complete answer:
The Wheatstone’s bridge condition states that if two or more parallel resistances in equal ratios have a parallel resistor across them, then the current flowing the latter will be zero.
Let us employ this condition in our circuit. We can see that the pair of resistances (R2, R1), (R4, R8) and (R6, R7) are in the ratio 1:2 to each other.
i.e., $\dfrac{R2}{R1}=\dfrac{R4}{R8}=\dfrac{R6}{R7}=\dfrac{1}{2}$
Thus, the Wheatstone’s bridge condition is valid here.
This gives in that the resistances R3 and R5 have no role in this circuit. The equivalent circuit will be –

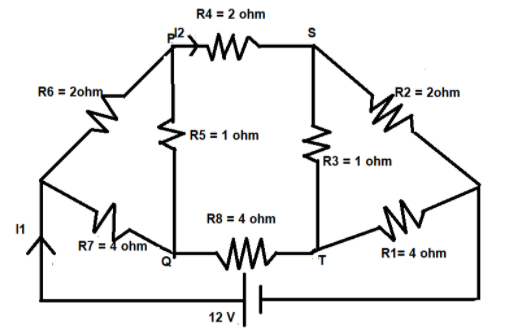
Now, let us calculate the equivalent resistance of the circuit. R2, R4, R6 and R1, R8, R7 are in series with each other.
i.e.,

& \Rightarrow {{R}_{s1}}=R2+R4+R6 \\\ & \text{ =2+2+2} \\\ & \text{ =6}\Omega \\\ & \text{ }and \\\ & \text{ }{{R}_{s2}}=R1+R8+R7 \\\ & \text{ = 4+4+4} \\\ & \text{ =12}\Omega \\\ & \dfrac{1}{{{R}_{eq}}}=\dfrac{1}{R}=\dfrac{1}{{{R}_{s1}}}+\dfrac{1}{{{R}_{s2}}} \\\ & \Rightarrow \dfrac{1}{R}=\dfrac{12+6}{6\times 12} \\\ & \Rightarrow R=4\Omega \\\ \end{aligned}$$ Now, we can find the current through the circuit. The total current ${I_1}$ is given by –$${I_1}=\dfrac{V}{R}=\dfrac{12}{4}=3A$$ --(1) Current ${I_2}$ is the current passing through the upper hand of the circuit. We can apply the current divider rule to find ${I_2}$. i.e., $$\begin{aligned} & \text{ }{I_1}={{I}_{total}}\times \dfrac{{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}} \\\ & \Rightarrow {I_2}={I_1}\times \dfrac{{{R}_{s2}}}{{{R}_{s1}}+{{R}_{s2}}} \\\ & \Rightarrow {I_2}=3\times \dfrac{12}{6+12} \\\ & \text{ =3}\times \dfrac{2}{3} \\\ & \therefore {I_2}=2A \\\ \end{aligned}$$ So, we can conclude that – a) The current ${I_1}$ is 3A. b) The current ${I_2}$ is 2A. c) Current doesn’t pass through PQ and ST. **The correct answers are given by options A, B and D.** **Note:** We can find the current in the circuit after applying Wheatstone’s condition using the Voltage-divider rule also. We find the voltages across the resistors in series connections and find the current in them. The method we have used is more convenient for this question. The points P, Q, S and T are equipotential points in the circuit.