Question

For the reaction, the initial mole $A$ is twice that of $B$. If at equilibrium moles of $B$ and $C$ are equal, then the percent of $B$ reacted is:
A. $10\%$
B. $20\%$
C. $40\%$
D. $60\%$

Answer 1

To solve the numerical one must be aware of basic concepts of ionic equilibrium. We can assume the initial condition $t = 0$ as given in the question. At equilibrium, some moles of the reactants will be reacted. So we will equate the concentration of $B$ and $C$. Finally, we will be able to calculate the percentage reacted using the general percentage formula.

Formula Used: Percentage of $B$ reacted
$\% B = \dfrac{X}{a} \times 100$
Where $X$ represents the moles of $B$ reacted at equilibrium,
$a$ represents the initial moles of $B$.

Complete step-by-step answer: For the reaction, Let us consider that initial concentration of $[B] = a$ and $[A] = 2a$. It is given that the initial mole $A$ is twice that of $B$.
Now we will consider the reaction at $t = 0$ and at equilibrium. So we can expres

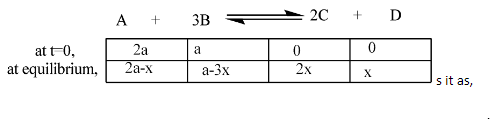
From the above analysis at equilibrium, we can conclude that at equilibrium $x$ moles are reacted from $A$ and $3x$ is reacted from $B$ and $2x$ is formed as $C$ with $x$ moles of $D$. The reactants are reacted and products are formed according to their stoichiometric coefficients.
Now according to the conditions given in the question equilibrium moles of $B$ and $C$ are equal. So we get,
$a - 3x = 2x$
$\Rightarrow x = \dfrac{a}{5}$
The mole of $B$ reacted is $3x$. So the moles of $B$ reacted are $\dfrac{{3a}}{5}$.
Now to find the percent of $B$ reacted we will use the formula,
$\% B = \dfrac{X}{a} \times 100$ Here, we have $X = \dfrac{{3a}}{5}$, after substituting we get,
$\Rightarrow \% B = \dfrac{{\dfrac{{3a}}{5}}}{a} \times 100$
$\% B = 60$
The percent of $B$ reacted is $60\%$

Therefore, the correct option is (D).

Note: We may make a mistake while writing the moles of the reactants and products at equilibrium. So check the coefficients of reactants and products when some moles from the reactants are reacted. The reaction leads to forward direction when we increase the amount of reactant.