Question

For the reaction $N_2(g) + O_2(g) \rightleftharpoons 2NO(g)$, the value of $K_c$ at $800^\circ C$ is $0.1$. When the equilibrium concentration of both the reactants is $0.5$ mol, the value of $K_p$ at this temperature is $x \times 10^{-3}$. Then what is $x$?

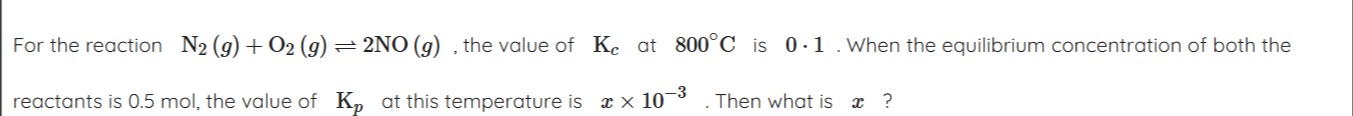
• A. 100
• B. 10
• C. 1
• D. 0.1

Answer 1

Answer: (A)

100

Answer 2

For the reaction $N_2(g) + O_2(g) \rightleftharpoons 2NO(g)$, the change in the number of moles of gas is $\Delta n = (\text{moles of gaseous products}) - (\text{moles of gaseous reactants}) = 2 - (1+1) = 0$. The relationship between $K_p$ and $K_c$ is given by $K_p = K_c (RT)^{\Delta n}$. Since $\Delta n = 0$, the equation simplifies to $K_p = K_c$. Given $K_c = 0.1$, therefore $K_p = 0.1$. The problem states that $K_p = x \times 10^{-3}$. So, $0.1 = x \times 10^{-3}$. Solving for $x$: $x = \frac{0.1}{10^{-3}} = 0.1 \times 10^3 = 100$. The equilibrium concentration of reactants is irrelevant when $\Delta n = 0$.