Question

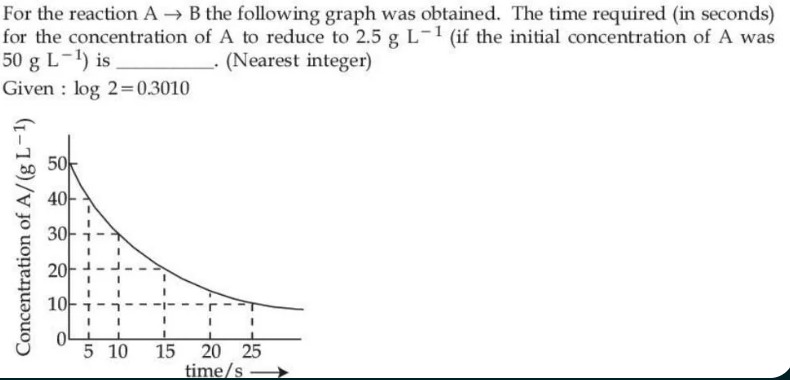
For the reaction A → B the following graph was obtained. The time required (in seconds) for the concentration of A to reduce to 2.5 g L$^{-1}$ (if the initial concentration of A was 50 g L$^{-1}$) is ________. (Nearest integer) Given : log 2 = 0.3010

Answer 1

28 s

Answer 2

For a first‐order reaction, the integrated rate law is

$$\ln \frac{[A]_0}{[A]} = k t.$$

Given that at $t = 15\,\text{s}$, $[A] = 10\,\text{g/L}$ with $[A]_0=50\,\text{g/L}$, we compute the rate constant $k$:

$$\ln \frac{50}{10} = \ln 5 = k \times 15 \quad\Longrightarrow\quad k = \frac{\ln 5}{15}.$$

To find the time when $[A] = 2.5\,\text{g/L}$:

$$\ln \frac{50}{2.5} = \ln 20 = k t.$$

Substitute $k$:

$$t = \frac{\ln 20}{\ln 5/15} = \frac{15\,\ln 20}{\ln 5}.$$

Using the relation $\ln20 = \ln5 + \ln4$ (and approximate values $\ln5 \approx 1.609$ and $\ln4 \approx 1.386$):

$$t \approx 15 \times \frac{1.609 + 1.386}{1.609} \approx 15 \times 1.861 \approx 27.91\,\text{s}.$$

Rounding to the nearest integer gives 28 s.