Question

For the principal values, evaluate ${{\tan }^{-1}}\left( -1 \right)+{{\cos }^{-1}}\left( \dfrac{-1}{\sqrt{2}} \right)$.

Answer 1

To solve the question given above, first we will draw the rough graphs of $y={{\tan }^{-1}}\left( x \right)$ and $y={{\cos }^{-1}}\left( x \right)$ and we will determine the nature of these graphs. Then we will find the value of ${{\tan }^{-1}}\left( -1 \right)$ in terms of ${{\tan }^{-1}}\left( 1 \right)$. And the values of ${{\cos }^{-1}}\left( \dfrac{-1}{\sqrt{2}} \right)$ in terms of ${{\cos }^{-1}}\left( \dfrac{1}{\sqrt{2}} \right)$. After that, we will find the value of ${{\tan }^{-1}}\left( -1 \right)+{{\cos }^{-1}}\left( \dfrac{-1}{\sqrt{2}} \right)$ by putting the respective values.

Complete step-by-step answer:
Before solving the question, we must know what is the nature of ${{\tan }^{-1}}\left( x \right)$ and ${{\cos }^{-1}}\left( x \right)$. For determining the nature of these inverse trigonometric functions, we will draw their respective graphs. The graph of ${{\tan }^{-1}}x$ is:

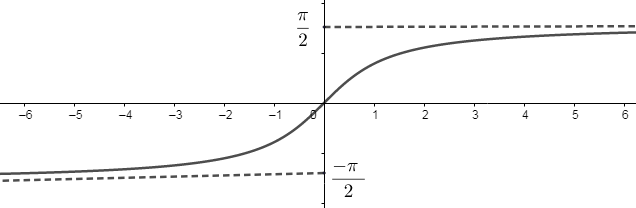
From the above graphs, we can see that the function ${{\tan }^{-1}}\left( x \right)$ is an odd function. If a function $f\left( x \right)$ is an odd function then we have the following relation:
So, ${{\tan }^{-1}}\left( -x \right)=-{{\tan }^{-1}}\left( x \right)$
Now, we will draw the graph of ${{\cos }^{-1}}\left( x \right)$:

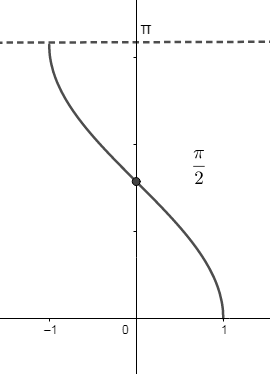
We can see from the above graph that ${{\cos }^{-1}}\left( -x \right)=\pi -{{\cos }^{-1}}\left( x \right)$.
Now, we will find the value of ${{\tan }^{-1}}\left( -1 \right)$. We know that,
We have shown above that ${{\tan }^{-1}}\left( -x \right)=-{{\tan }^{-1}}\left( x \right)$ so using this relation in solving ${{\tan }^{-1}}\left( -1 \right)$ we get,
${{\tan }^{-1}}\left( -1 \right)=-{{\tan }^{-1}}\left( 1 \right)$…………. Eq. (1)
We know that, the principal value for ${{\tan }^{-1}}\left( 1 \right)$ is equal to:
$\dfrac{\pi }{4}$
So, substituting this principal value in eq. (1) we get,
${{\tan }^{-1}}\left( -1 \right)=-\dfrac{\pi }{4}$……… Eq. (2)
Now, we will find the value of ${{\cos }^{-1}}\left( -\dfrac{1}{\sqrt{2}} \right)$. We have shown above the following relation:
${{\cos }^{-1}}\left( -x \right)=\pi -{{\cos }^{-1}}\left( x \right)$ so using this relation in ${{\cos }^{-1}}\left( -\dfrac{1}{\sqrt{2}} \right)$ we get,
${{\cos }^{-1}}\left( \dfrac{-1}{\sqrt{2}} \right)=\pi -{{\cos }^{-1}}\left( \dfrac{1}{\sqrt{2}} \right)$……… Eq. (3)
We know that the principal value for:
${{\cos }^{-1}}\left( \dfrac{1}{\sqrt{2}} \right)=\dfrac{\pi }{4}$
On putting the value of ${{\cos }^{-1}}\left( \dfrac{-1}{\sqrt{2}} \right)$ in eq. (3), we will get:
${{\cos }^{-1}}\left( \dfrac{-1}{\sqrt{2}} \right)=\pi -\dfrac{\pi }{4}$
$\Rightarrow {{\cos }^{-1}}\left( \dfrac{-1}{\sqrt{2}} \right)=\dfrac{3\pi }{4}$ ……… Eq. (4)
Now, we will add equations (2) and (4). After doing this, we will get:

& {{\tan }^{-1}}\left( -1 \right)+{{\cos }^{-1}}\left( \dfrac{-1}{\sqrt{2}} \right)=\dfrac{-\pi }{4}+\dfrac{3\pi }{4} \\\ & \Rightarrow {{\tan }^{-1}}\left( -1 \right)+{{\cos }^{-1}}\left( \dfrac{-1}{\sqrt{2}} \right)=\dfrac{\pi }{2} \\\ \end{aligned}$$ **Note:** The above question can be solved in an alternate way as shown: We know that $$\cos \dfrac{\pi }{4}=\dfrac{1}{\sqrt{2}}$$$$\Rightarrow {{\cos }^{-1}}\left( \dfrac{1}{\sqrt{2}} \right)=\dfrac{\pi }{4}$$. Now, we can also say that, $${{\cot }^{-1}}\left( 1 \right)=\dfrac{\pi }{4}$$. Now, $${{\cos }^{-1}}\left( \dfrac{1}{\sqrt{2}} \right)={{\cot }^{-1}}\left( 1 \right)$$. Now, we will subtract $$\pi $$ on both sides. Thus we will get: $$\begin{aligned} & {{\cos }^{-1}}\left( \dfrac{1}{\sqrt{2}} \right)-\pi ={{\cot }^{-1}}\left( 1 \right)-\pi \\\ & \Rightarrow \pi -{{\cos }^{-1}}\left( \dfrac{1}{\sqrt{2}} \right)=\pi -{{\cot }^{-1}}\left( 1 \right) \\\ & \Rightarrow {{\cos }^{-1}}\left( -\dfrac{1}{\sqrt{2}} \right)={{\cot }^{-1}}\left( -1 \right) \\\ \end{aligned}$$ Now the value of $${{\tan }^{-1}}\left( -1 \right)+{{\cos }^{-1}}\left( \dfrac{-1}{\sqrt{2}} \right)$$ = $${{\tan }^{-1}}\left( -1 \right)+{{\cot }^{-1}}\left( -1 \right)$$. Now we will apply the identity: $${{\cot }^{-1}}\left( -1 \right)+{{\tan }^{-1}}\left( -1 \right)=\dfrac{\pi }{2}$$. So, we will get, $${{\tan }^{-1}}\left( -1 \right)+{{\cos }^{-1}}\left( \dfrac{-1}{\sqrt{2}} \right)=\dfrac{\pi }{2}$$.