Question

For the principal value, evaluate the following
${{\sin }^{-1}}\left[ \cos \left( 2{{\operatorname{cosec}}^{-1}}\left( -2 \right) \right) \right]$

Answer 1

Hint:First of all, use ${{\operatorname{cosec}}^{-1}}\left( -x \right)=-{{\operatorname{cosec}}^{-1}}x$ and then use a trigonometric table to find the value of ${{\operatorname{cosec}}^{-1}}\left( 2 \right)$. Now use $\cos \left( -\theta \right)=\cos \theta$ and again use the table to find the value of $\cos \dfrac{\pi }{3}$. Find the angle at which $\sin \theta =\dfrac{1}{2}$ from the table or the value of ${{\sin }^{-1}}\left( \dfrac{1}{2} \right)$ to get the required answer.

Complete step-by-step answer:
In this question, we have to find the principal value of ${{\sin }^{-1}}\left[ \cos \left( 2{{\operatorname{cosec}}^{-1}}\left( -2 \right) \right) \right]$.
First of all, let us consider the expression given in the question,
$E={{\sin }^{-1}}\left[ \cos \left( 2{{\operatorname{cosec}}^{-1}}\left( -2 \right) \right) \right]$
We know that, ${{\operatorname{cosec}}^{-1}}\left( -x \right)=-{{\operatorname{cosec}}^{-1}}x$. By using this in the above expression, we get,
$E={{\sin }^{-1}}\left[ \cos \left( -2{{\operatorname{cosec}}^{-1}}2 \right) \right]....\left( i \right)$
Now, let us draw the table for trigonometric ratios of general angles.

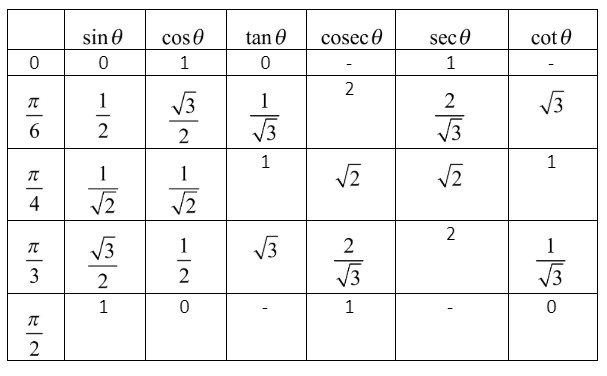
From the above table, we can see that,
$\operatorname{cosec}\left( \dfrac{\pi }{6} \right)=2$
$\Rightarrow {{\operatorname{cosec}}^{-1}}\left( 2 \right)=\dfrac{\pi }{6}$
So, by substituting the value of ${{\operatorname{cosec}}^{-1}}\left( 2 \right)$ in the expression (i), we get,
$E={{\sin }^{-1}}\left[ \cos \left( -2.\dfrac{\pi }{6} \right) \right]$
$E={{\sin }^{-1}}\left[ \cos \left( -\dfrac{\pi }{3} \right) \right]$
We know that, $\cos \left( -\theta \right)=\cos \theta$. By using this in the above expression, we get,
$E={{\sin }^{-1}}\left[ \cos \dfrac{\pi }{3} \right]$
Now, from the trigonometric table, we can see that, $\cos \dfrac{\pi }{3}=\dfrac{1}{2}$. So, by substituting the value of $\cos \dfrac{\pi }{3}$ in the above expression, we get,
$E={{\sin }^{-1}}\left( \dfrac{1}{2} \right)....\left( ii \right)$
Now we know that the range of principal value of ${{\sin }^{-1}}\left( x \right)$ lies between $\left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right]$.
From the table of general trigonometric ratios, we get,
$\sin \left( \dfrac{\pi }{6} \right)=\dfrac{1}{2}$
$\Rightarrow {{\sin }^{-1}}\left( \dfrac{1}{2} \right)=\dfrac{\pi }{6}$
Now by substituting the value of ${{\sin }^{-1}}\left( \dfrac{1}{2} \right)$ in the expression (ii), we get,
$E=\dfrac{\pi }{6}$
Hence, we get the value of ${{\sin }^{-1}}\left[ \cos \left( 2{{\operatorname{cosec}}^{-1}}\left( -2 \right) \right) \right]$ as $\dfrac{\pi }{6}$.

Note: In this question, students must take care that the value of the angle must lie in the range of ${{\operatorname{cosec}}^{-1}}x$ which is \left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right]-\left\\{ 0 \right\\} and ${{\sin }^{-1}}x$ which is $\left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right]$ accordingly. Also, students can verify their answer by equating the given expression with $\dfrac{\pi }{6}$ and taking sin on both sides and keep solving until LHS = RHS.