Solveeit Logo
Login

Question

Question: For the principal value, evaluate the following \[{{\sin }^{-1}}\left( -\dfrac{\sqrt{3}}{2} \right...

For the principal value, evaluate the following
sin⁡−1(−32)+cosec⁡−1(−23){{\sin }^{-1}}\left( -\dfrac{\sqrt{3}}{2} \right)+{{\operatorname{cosec}}^{-1}}\left( -\dfrac{2}{\sqrt{3}} \right).

Explanation

Solution

Hint:First of all, use cosec⁡−1(−x)=−cosec⁡−1x{{\operatorname{cosec}}^{-1}}\left( -x \right)=-{{\operatorname{cosec}}^{-1}}x and sin⁡−1(−x)=−sin⁡−1x{{\sin }^{-1}}\left( -x \right)=-{{\sin }^{-1}}x to simplify the given expression. Now from the trigonometric table, find the value of θ\theta at which sin⁡θ=32\sin \theta =\dfrac{\sqrt{3}}{2} and cosec⁡θ=23\operatorname{cosec}\theta =\dfrac{2}{\sqrt{3}} or the value of sin⁡−1(32){{\sin }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right) and cosec⁡−1(23){{\operatorname{cosec}}^{-1}}\left( \dfrac{2}{\sqrt{3}} \right) and substitute these in the given expression to get the required value.

Complete step-by-step answer:
In this question, we have to find the principal value of sin⁡−1(−32)+cosec⁡−1(−23){{\sin }^{-1}}\left( -\dfrac{\sqrt{3}}{2} \right)+{{\operatorname{cosec}}^{-1}}\left( -\dfrac{2}{\sqrt{3}} \right).
First of all, let us consider the expression given in the question,
E=sin⁡−1(−32)+cosec⁡−1(−23)E={{\sin }^{-1}}\left( -\dfrac{\sqrt{3}}{2} \right)+{{\operatorname{cosec}}^{-1}}\left( -\dfrac{2}{\sqrt{3}} \right)
We know that, sin⁡−1(−x)=−sin⁡−1x{{\sin }^{-1}}\left( -x \right)=-{{\sin }^{-1}}x. By using this in the above expression, we get,
E=−sin⁡−1(32)+cosec⁡−1(−23)E=-{{\sin }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right)+{{\operatorname{cosec}}^{-1}}\left( -\dfrac{2}{\sqrt{3}} \right)
We know that, cosec⁡−1(−x)=−cosec⁡−1x{{\operatorname{cosec}}^{-1}}\left( -x \right)=-{{\operatorname{cosec}}^{-1}}x. By using this in the above expression, we get,
E=−sin⁡−1(32)−cosec⁡−1(23).....(i)E=-{{\sin }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right)-{{\operatorname{cosec}}^{-1}}\left( \dfrac{2}{\sqrt{3}} \right).....\left( i \right)
Now, let us draw the table for trigonometric ratios of general angles.

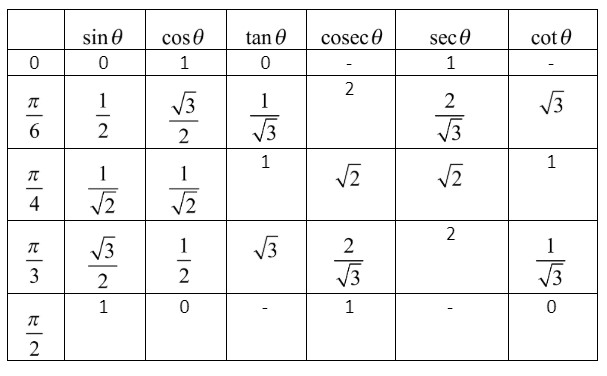
Now we know that the range of principal value of sin⁡−1(x){{\sin }^{-1}}\left( x \right) lies between [−π2,π2]\left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right].
From the table of general trigonometric ratios, we get,
sin⁡(π3)=32\sin \left( \dfrac{\pi }{3} \right)=\dfrac{\sqrt{3}}{2}
By taking sin⁡−1{{\sin }^{-1}} on both the sides, we get,
sin⁡−1sin⁡(π3)=sin⁡−1(32){{\sin }^{-1}}\sin \left( \dfrac{\pi }{3} \right)={{\sin }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right)
We know that for −π2≤x≤π2,sin⁡−1sin⁡(x)=x\dfrac{-\pi }{2}\le x\le \dfrac{\pi }{2},{{\sin }^{-1}}\sin \left( x \right)=x. So, we get,
π3=sin⁡−1(32)...(ii)\dfrac{\pi }{3}={{\sin }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right)...\left( ii \right)
Now, we also know that the range of principal value of cosec⁡−1x{{\operatorname{cosec}}^{-1}}x lies between \left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right]-\left\\{ 0 \right\\}
From the table of trigonometric ratios, we get,
cosec⁡(π3)=23\operatorname{cosec}\left( \dfrac{\pi }{3} \right)=\dfrac{2}{\sqrt{3}}
By taking cosec⁡−1{{\operatorname{cosec}}^{-1}} on both the sides, we get,
cosec⁡−1(cosec⁡(π3))=cosec⁡−1(23){{\operatorname{cosec}}^{-1}}\left( \operatorname{cosec}\left( \dfrac{\pi }{3} \right) \right)={{\operatorname{cosec}}^{-1}}\left( \dfrac{2}{\sqrt{3}} \right)
We know that for \left[ \dfrac{-\pi }{2}\le x\le \dfrac{\pi }{2} \right]-\left\\{ 0 \right\\},{{\operatorname{cosec}}^{-1}}\operatorname{cosec}\left( x \right)=x. So, we get,
π3=cosec⁡−1(23)....(iii)\dfrac{\pi }{3}={{\operatorname{cosec}}^{-1}}\left( \dfrac{2}{\sqrt{3}} \right)....\left( iii \right)
So, by substituting the value of cosec⁡−1(23){{\operatorname{cosec}}^{-1}}\left( \dfrac{2}{\sqrt{3}} \right) from equation (iii) and sin⁡−1(32){{\sin }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right) from equation (ii) in equation (i), we get,
E=−π3−π3E=-\dfrac{\pi }{3}-\dfrac{\pi }{3}
E=−2π3E=\dfrac{-2\pi }{3}
Hence, we get the value of sin⁡−1(−32)+cosec⁡−1(−23){{\sin }^{-1}}\left( -\dfrac{\sqrt{3}}{2} \right)+{{\operatorname{cosec}}^{-1}}\left( -\dfrac{2}{\sqrt{3}} \right) as −2π3\dfrac{-2\pi }{3}.

Note: In this question, many students make this mistake of taking cosec⁡−1(−x){{\operatorname{cosec}}^{-1}}\left( -x \right) as π−cosec⁡−1(x)\pi -{{\operatorname{cosec}}^{-1}}\left( x \right) like that in case of sec⁡−1(−x){{\sec }^{-1}}\left( -x \right) and cot⁡−1(−x){{\cot }^{-1}}\left( -x \right) which is wrong because cosec⁡−1(−x)=−cosec⁡−1(x){{\operatorname{cosec}}^{-1}}\left( -x \right)=-{{\operatorname{cosec}}^{-1}}\left( x \right).Students must strictly take care of the domain and range of the inverse trigonometric functions. Also, students must take care that the angle they take must lie in the range of the respective trigonometric functions to get the required answer.