Question

For the network shown in the figure the current $i$ is:
A. $\dfrac{{18V}}{5}$
B. $\dfrac{{5V}}{9}$
C. $\dfrac{{9V}}{{35}}$
D. $\dfrac{{5V}}{{18}}$

Answer 1

To find the current in the circuit we need to find the equivalent resistance that is present in the circuit and we can see here that this is a Wheatstone bridge circuit and we know that a Wheatstone bridge is an electrical circuit used to measure an unknown electrical resistance by balancing two legs of a bridge circuit, one leg of which includes the unknown component. The primary benefit of the circuit is its ability to provide extremely accurate measurements. After finding the equivalent resistance we will find the current by applying Ohm’s law.

Complete step by step solution:
According to the question, Let’s say,
$P = 4\Omega ,Q = 2\Omega ,R = 6\Omega ,S = 3\Omega$
According to the Wheatstone bridge circuit here,
$\dfrac{P}{Q} = \dfrac{R}{S}$
So, it is the balanced condition and no current flow the middle resistance i.e., $4\Omega$,
Thus, we can remove from the circuit, and the new circuit will become as below,

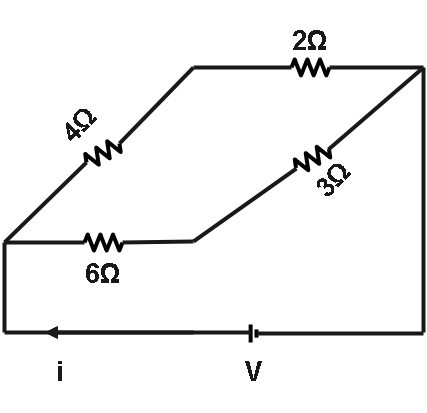
Now, here we can see the circuit is series and parallel and can solve for the equivalence resistance.
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} \\\ \Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{{{R_1} + {R_2}}}{{{R_1} \times {R_2}}} \\\ \Rightarrow {R_{eq}} = \dfrac{{{R_1} \times {R_2}}}{{{R_1} + {R_2}}} \\\$
Now, substituting the value according to the circuit,
${R_{eq}} = \dfrac{{{R_1} \times {R_2}}}{{{R_1} + {R_2}}} \\\ \Rightarrow {R_{eq}} = \dfrac{{6 \times 9}}{{6 + 9}} \\\ \Rightarrow {R_{eq}} = \dfrac{{54}}{{15}} \\\ \Rightarrow {R_{eq}} = \dfrac{{18}}{5} \\\$
Now, applying Ohm’s law to find the current,
$\because V = IR \\\ \Rightarrow I = \dfrac{V}{R} \\\$
Now, substituting the values,
$I = \dfrac{V}{R} \\\ \Rightarrow I = \dfrac{{5V}}{{18}} \\\$
So, for the network shown in the figure the current $i$ is $\dfrac{{5V}}{{18}}$ .
Hence, the correct option is D.

Note:
In this type of question when you see there is a Wheatstone bridge circuit apply the application and solve for the equivalent resistance and after find out the required solution what is asked in the question and Ohm's law states that the current through a conductor between two points is directly proportional to the voltage across the two points.