Question

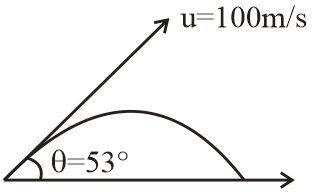
For the given projectile as shown, the time $($in seconds$)$ after which the angle between velocity vector and initial velocity vector becomes $\dfrac{\pi }{2}$ is $(u = 100m/s)$

(A) $\dfrac{{50}}{4}$
(B) $\dfrac{{100}}{3}$
(C) $\dfrac{{14}}{3}$
(D) $\dfrac{{28}}{3}$

Answer 1

In order to solve above problem first calculate, the initial velocity vector component in x and y direction i.e.,
${u_x} = u\cos \theta$
${u_y} = u\sin \theta$
$u =$Initial velocity vector
${u_x} =$x component of Initial velocity vector
${u_y} =$y component of Initial velocity vector
After then calculate the velocity vector at time t and also calculate the velocity vector component in x and y direction with the help of newton’s first equation. Now, on comparing the both velocity components, we will get a desired solution.

Complete step by step answer:
Given that initial velocity $u = 100m/s$ and the angle at which the particle is projected initially is $\theta = 53^\circ$.
So, x-component of initial velocity ${u_x} = u\cos \theta$
${u_x} = 100\cos 53^\circ$
$\Rightarrow {u_x} = 100\left( {\dfrac{3}{5}} \right)$ $\left[ {\because \cos 53^\circ = \dfrac{3}{5}} \right]$
$\Rightarrow {u_x} = \dfrac{{300}}{5}$
$\Rightarrow {u_x} = 60$ …..(1)
And y-component of initial velocity ${u_y} = u\sin \theta$
${u_y} = 100sin53^\circ$
$\Rightarrow {u_y} = 100\left( {\dfrac{4}{5}} \right)$ $\left[ {\because \sin 53^\circ = \dfrac{4}{5}} \right]$
$\Rightarrow {u_y} = \dfrac{{400}}{5}$
$\Rightarrow {u_y} = 80$ …..(2)
Now, according to the given in question the angle between velocity vector at time t and initial velocity vector becomes $\dfrac{\pi }{2}$ i.e., 90. Here we can easily understand this thing with diagram as –

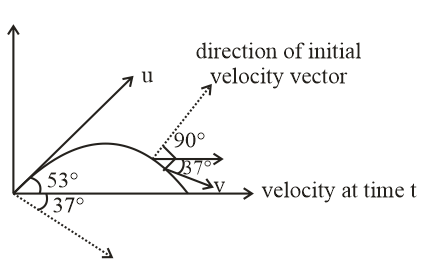
In the diagram we can easily see that at time t the angle of velocity vector $(\overrightarrow v )$ with horizontal as $37^\circ$.
So, the x-component of velocity vector $\overrightarrow v$ is
${v_x} = v\cos \theta$ $[$Here $\theta = 37^\circ ]$
We know that the x-component of velocity does not change during the whole motion of the projectile because acceleration in x-direction is zero.
Here ${v_x} =$x component of velocity vector$v$at time$t$
So, ${v_x} = {u_x}$
So, from equation 1
$\Rightarrow {v_x} = 60$
So, $v\cos 37^\circ = 60$
$\Rightarrow v = \dfrac{{60}}{{\cos 37^\circ }}$
$\because \cos 37^\circ = \dfrac{4}{5}$
$\Rightarrow v = \dfrac{{60 \times 5}}{4}$
$\Rightarrow v = \dfrac{{300}}{4}$
$\Rightarrow v = 75m/s$
Hence, the velocity at time t is 75m/s
Now, the y-component of velocity vector at time t is
${v_y} = - v\sin 37^\circ$
$\Rightarrow {v_y} = - \left( {75 \times \dfrac{3}{5}} \right)$ $\left[ {\because \sin 37^\circ = \dfrac{3}{5}} \right]$
$\Rightarrow {v_y} = - (15 \times 3)$
$\Rightarrow {v_y} = - 45$ …..(3)
Here –ve sign represents the downward direction.
So, we can write newton’s first equation for y-component of velocity vector at time t as
${v_y} = {u_y} + {a_y}t$
Here ${a_y} =$acceleration in y direction
$\because {a_y} = - g = - 10m/{s^2}$
So, from equation 2 and 3
$\Rightarrow - 45 = 80 - 10t$
$\Rightarrow - 45 - 80 = - 10t$
$\Rightarrow t = \dfrac{{ - 125}}{{ - 10}}$
$\Rightarrow t = \dfrac{{125}}{{10}}$
$\Rightarrow t = \dfrac{{25}}{2}\sec$
Now divide and multiply with 2 then
$t = \dfrac{{25 \times 2}}{{2 \times 2}}$
$\Rightarrow t = \dfrac{{50}}{4}\sec$

Therefore, option A is the correct answer.

Note:
Alternatively,
We know that, the x-component of initial velocity is
${u_x} = u\cos \theta$

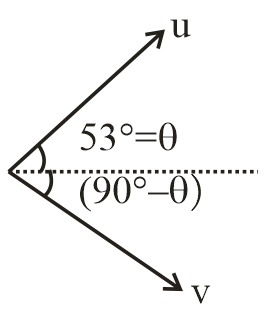
The y-component of initial velocity is
${u_y} = u\sin \theta$
So, initial velocity vector
$\overrightarrow u = {u_x}\widehat i + {u_y}\widehat j$
$\overrightarrow u = (u\cos \theta )\widehat i + (u\sin \theta )\widehat j$ …..(1)
At time t, the velocity vector is given as
$\overrightarrow v = {v_x}\widehat i + {v_y}\widehat j$
Here ${v_x} = v\cos (90 - \theta ) = v\sin \theta$
Because x-component of velocity does not changes
So, ${v_x} = {u_x}$
Now, from newton’s first equation
${v_y} = ({u_y} - gt)$
So, $\overrightarrow v = {u_x}\widehat i + ({u_y} - gt)\widehat j$
$\overrightarrow v = (u\cos \theta )\widehat i + (u\sin \theta - gt)\widehat j$ …..(2)
Given that at time t, $\overrightarrow v$ and $\overrightarrow u$ are perpendicular to each other.
So, $\overrightarrow u \cdot \overrightarrow v = 0$
From equation 1 and 2
$[(u\cos \theta )\widehat i + (u\sin \theta )\widehat j] \cdot [(u\cos \theta )\widehat i + (u\sin \theta - gt)\widehat j] = 0$
${u^2}{\cos ^2}\theta + (u\sin \theta )(u\sin \theta - gt) = 0$
$\implies {u^2}{\cos ^2}\theta + {u^2}{\sin ^2}\theta - ugt\sin \theta = 0$
$\implies {u^2}({\cos ^2}\theta + {\sin ^2}\theta ) = ugt\sin \theta$
$\implies {\cos ^2}\theta + {\sin ^2}\theta = 1$
$\implies {u^2} = ugt\sin \theta$
$\implies t = \dfrac{{{u^2}}}{{ug\sin \theta }}$
$\implies t = \dfrac{u}{{g\sin \theta }}$
Here u = initial velocity vector
g = acceleration due to gravity
given that
$u = 100m/s$
$g = 10m/{s^2}$
$\theta = 53^\circ$
So, $t = \dfrac{{100}}{{10\sin 53^\circ }}$
$\because \sin 53^\circ = \dfrac{4}{5}$
$t = \dfrac{{100}}{{10 \times \dfrac{4}{5}}}$
$\implies t = \dfrac{{10 \times 5}}{4}$
$\therefore t = \dfrac{{50}}{4}\sec$