Question

For the given parabola find the coordinates of focus, axis, the equation of the directrix, and the length of the latus rectum.
${{x}^{2}}=-9y$

Answer 1

Hint: Compare the equation of the parabola ${{x}^{2}}=-9y$ with the standard equation of the parabola and get the value of a. The axis of the parabola ${{x}^{2}}=-4ay$ is the y-axis. We know that for the parabola ${{x}^{2}}=-4ay$ , the coordinate of the focus is $\left( 0,-a \right)$ , the equation of the directrix is $y=a$ , the length of the latus rectum is 4a. Now, using the value of $a$ get the coordinates of focus, axis, the equation of the directrix, and the length of the latus rectum.

Complete step-by-step answer:
According to the question, we have a parabola and we have to find the coordinates of focus, axis, the equation of the directrix, and the length of the latus rectum.
The equation of the parabola, ${{x}^{2}}=-9y$ ……………………………(1)

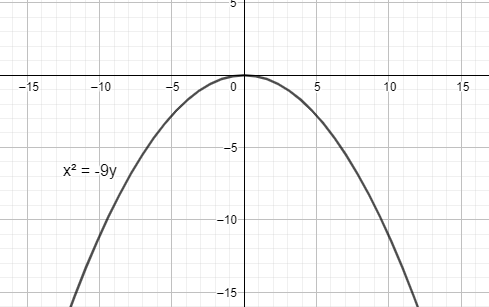
The given equation of the parabola is on the form of the standard equation of the parabola ${{x}^{2}}=-4ay$ ………………………(2)
Now, on comparing equation (1) and equation (2), we get

& \Rightarrow -4ay=-9y \\\ & \Rightarrow 4ay=9y \\\ & \Rightarrow 4a=9 \\\ \end{aligned}$$ $$\Rightarrow a=\dfrac{9}{4}$$ ………………………….(3) We know that for the parabola $${{x}^{2}}=-4ay$$ , the coordinate of the focus is $$\left( 0,-a \right)$$ ………………………(4) From equation (3), we have the value of a, $$a=\dfrac{9}{4}$$ . Now, putting the value of $$a$$ in equation (4), we get The coordinate of the focus is $$\left( 0,-\dfrac{9}{4} \right)$$ ………………………………….(5) We also know that for the parabola $${{x}^{2}}=-4ay$$ , the equation of the directrix is $$y=a$$ ………………………..(6) From equation (3), we have the value of a, $$a=\dfrac{9}{4}$$ . Now, putting the value of $$a$$ in equation (6), we get The equation of the directrix is $$y=\dfrac{9}{4}$$ ………………………………………….(7) We know the formula for the length of latus rectum, Latus rectum = $$4a$$ …………………………………..(8) From equation (3), we have the value of a, $$a=\dfrac{9}{4}$$ . Now, putting the value of $$a$$ in equation (8), we get The length of latus rectum, Latus rectum = $$4a=4\times \dfrac{9}{4}=9$$ …………………………………….(10) We know that the axis of the parabola $${{x}^{2}}=-4ay$$ is the y-axis. Since the parabola $${{x}^{2}}=-9y$$ is of the form $${{x}^{2}}=-4ay$$ so, the axis of the parabola $${{x}^{2}}=-9y$$ is also the y-axis and the equation of the y-axis is $$x=0$$ …………………………..(12) Now, from equation (5), equation (7), equation (10), and equation (11), we have The coordinate of the focus is $$\left( 0,-\dfrac{9}{4} \right)$$ . The equation of the directrix is $$y=\dfrac{9}{4}$$ . The length of the latus rectum, Latus rectum = 9. The axis of the parabola is the y-axis i.e, $$x=0$$ . Note: In this question, one might compare the equation of the parabola $${{x}^{2}}=-9y$$ with the standard form that is, $${{y}^{2}}=4ax$$ . This is wrong because the equation of the parabola $${{x}^{2}}=-9y$$ is not in the form of the equation of the parabola, $${{y}^{2}}=4ax$$ . The given equation of the parabola $${{x}^{2}}=-9y$$ is in the form of the standard equation of the parabola $${{x}^{2}}=-4ay$$ . So, we have to compare the equations $${{x}^{2}}=-9y$$ and $${{x}^{2}}=-4ay$$ .