Question

For the given orbital in column ${\rm{I}}$, the only CORRECT combination for any hydrogen like species is-

Column 1	Column 2	Column 3
${\rm{(I)}}$ ${\rm{1s}}$orbital	{\rm{(i)}}$$$${{\rm{\varphi }}_{{\rm{n,l,}}{{\rm{m}}_{\rm{l}}}}}\propto {\left( {\dfrac{{\rm{Z}}}{{{{\rm{a}}_{\rm{0}}}}}} \right)^{\dfrac{{\rm{3}}}{{\rm{2}}}}}{{\rm{e}}^{\rm{ - }}}^{\left( {\dfrac{{{\rm{Zr}}}}{{{{\rm{a}}_{\rm{0}}}}}} \right)}	(P)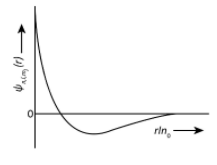
${\rm{(II)}}$ ${\rm{2s}}$orbital	${\rm{(ii)}}$one radial node	(Q) Probability density at nucleus
${\rm{(III)}}$ ${\rm{2}}{{\rm{p}}_z}$orbital	{\rm{(iii)}}$$$${{\rm{\varphi }}_{{\rm{n,l,}}{{\rm{m}}_{\rm{l}}}}}\propto {\left( {\dfrac{{\rm{Z}}}{{{{\rm{a}}_{\rm{0}}}}}} \right)^{\dfrac{5}{{\rm{2}}}}}{\rm{r}}{{\rm{e}}^{\rm{ - }}}^{\left( {\dfrac{{{\rm{Zr}}}}{{{\rm{2}}{{\rm{a}}_{\rm{0}}}}}} \right)}{\mathop{\rm co}\nolimits} {\rm{s\theta }}	(R) Probability density is maximum at nucleus
{\rm{(IV)}}$$$${\rm{3d}}_z^2orbital	{\rm{(iv)}}$$$${\rm{xy}}plane is a nodal node	(S) Energy needed to excite electrons from $n\, = \,2$ state to $n\, = \,4$ state is $\dfrac{{27}}{{32}}$times energy needed to excite electrons from $n\, = \,2$ state to $n\, = \,6$ state

(A) {\rm{(IV)}}$$$${\rm{(iv)}}(R)
(B) {\rm{(III)}}$$$${\rm{(iii)}} (P)
(C) {\rm{(II)}}$$$${\rm{(ii)}}(P)
(D) {\rm{(I)}}$$$${\rm{(ii)}}(S)

Answer 1

As we know that hydrogen is the simplest atom containing only one electron. ${\rm{n,}}\,{\rm{l,}}\,{{\rm{m}}_{\rm{l}}}$ resembles the principal quantum number, azimuthal quantum number and magnetic quantum number respectively. Radial node is measured from ${\rm{n}}\,{\rm{l}}$ values. The probability density of finding the electron is never $100\%$ because electrons are having Heisenberg uncertainty principle.

Complete answer
We will see the column one by one
In column 1, we will determine the radial nodes of the given orbitals by the formula
${\rm{radial}}\,{\rm{node = }}\,{\rm{n - l - 1}}$
For ${\rm{1s}}$orbital
${\rm{radial}}\,{\rm{node}}\,{\rm{ = }}\,1{\rm{ - 0 - 1 = }}\,0$
For ${\rm{2s}}$orbital
${\rm{radial}}\,{\rm{node}}\,{\rm{ = }}\,2{\rm{ - 0 - 1 = }}\,1$
For ${\rm{3}}{{\rm{p}}_z}$orbital
${\rm{radial}}\,{\rm{node}}\,{\rm{ = }}\,{\rm{3 - 1 - 1 = }}\,{\rm{1}}$
For ${\rm{3d}}_z^2$orbital
${\rm{radial}}\,{\rm{node}}\,{\rm{ = }}\,3{\rm{ - 2 - 1 = }}\,0$
Now we could see from above explanation, the radial nodes is one for ${\rm{2s}}$ and ${\rm{3}}{{\rm{p}}_z}$ orbitals but the graph for ${\rm{2s}}$orbital is shown as
By the formula

$${{\rm{R}}_{{\rm{2,0}}}}{\rm{ = }}\dfrac{{\rm{1}}}{{\sqrt {{\rm{32\pi }}} }}\dfrac{{\rm{1}}}{{{\rm{a}}_{\rm{0}}^{\dfrac{{\rm{3}}}{{\rm{2}}}}}}\left( {{\rm{2 - }}\dfrac{{\rm{r}}}{{{{\rm{a}}_{\rm{0}}}}}} \right){{\rm{e}}^{\rm{ - }}}^{\left( {\dfrac{{\rm{r}}}{{{\rm{2}}{{\rm{a}}_{\rm{0}}}}}} \right)}\\\ {\rm{y = }}\left( {{\rm{2 - x}}} \right)\,{{\rm{e}}^{{\rm{ - x}}}}$$

Appling above formula we have values along ${\rm{x}}$and ${\rm{y}}$ direction as-

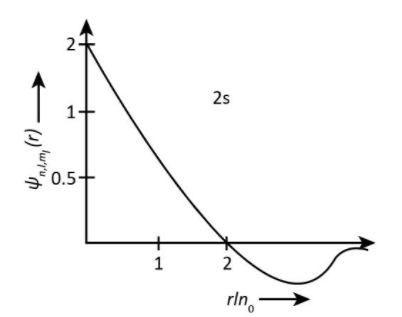
And the graph for ${\rm{3}}{{\rm{p}}_z}$orbital is shown as-

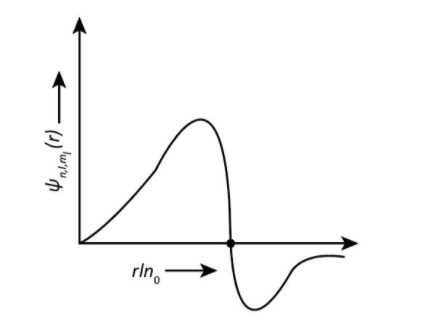
**Therefore, our correct option is option (C) -{\rm{(II)}}$$$${\rm{(ii)}}(P).

Note: **
${{\rm{\varphi }}_{{\rm{n,l,}}{{\rm{m}}_{\rm{l}}}}}\propto {\left( {\dfrac{{\rm{Z}}}{{{{\rm{a}}_{\rm{0}}}}}} \right)^{\dfrac{{\rm{3}}}{{\rm{2}}}}}{{\rm{e}}^{\rm{ - }}}^{\left( {\dfrac{{{\rm{Zr}}}}{{{{\rm{a}}_{\rm{0}}}}}} \right)}$ belongs to orbital ${\rm{1s}}$ where principle quantum number can be calculated by ${{\rm{e}}^{\rm{ - }}}^{\left( {\dfrac{{{\rm{Zr}}}}{{{{\rm{a}}_{\rm{0}}}}}} \right)}$ and azimuthal quantum number is calculated by minimum power of ${\rm{r}}$ or maximum power of ${\rm{sin\theta cos\theta }}$.
Energy of one- dimensional box is calculated by –
${{\rm{E}}_{\rm{x}}}{\rm{ = }}\dfrac{{{\rm{n}}_{\rm{x}}^{\rm{2}}{{\rm{h}}^{\rm{2}}}}}{{{\rm{8m}}{{\rm{l}}^{\rm{2}}}}}$